What's the height of the pyramid ?
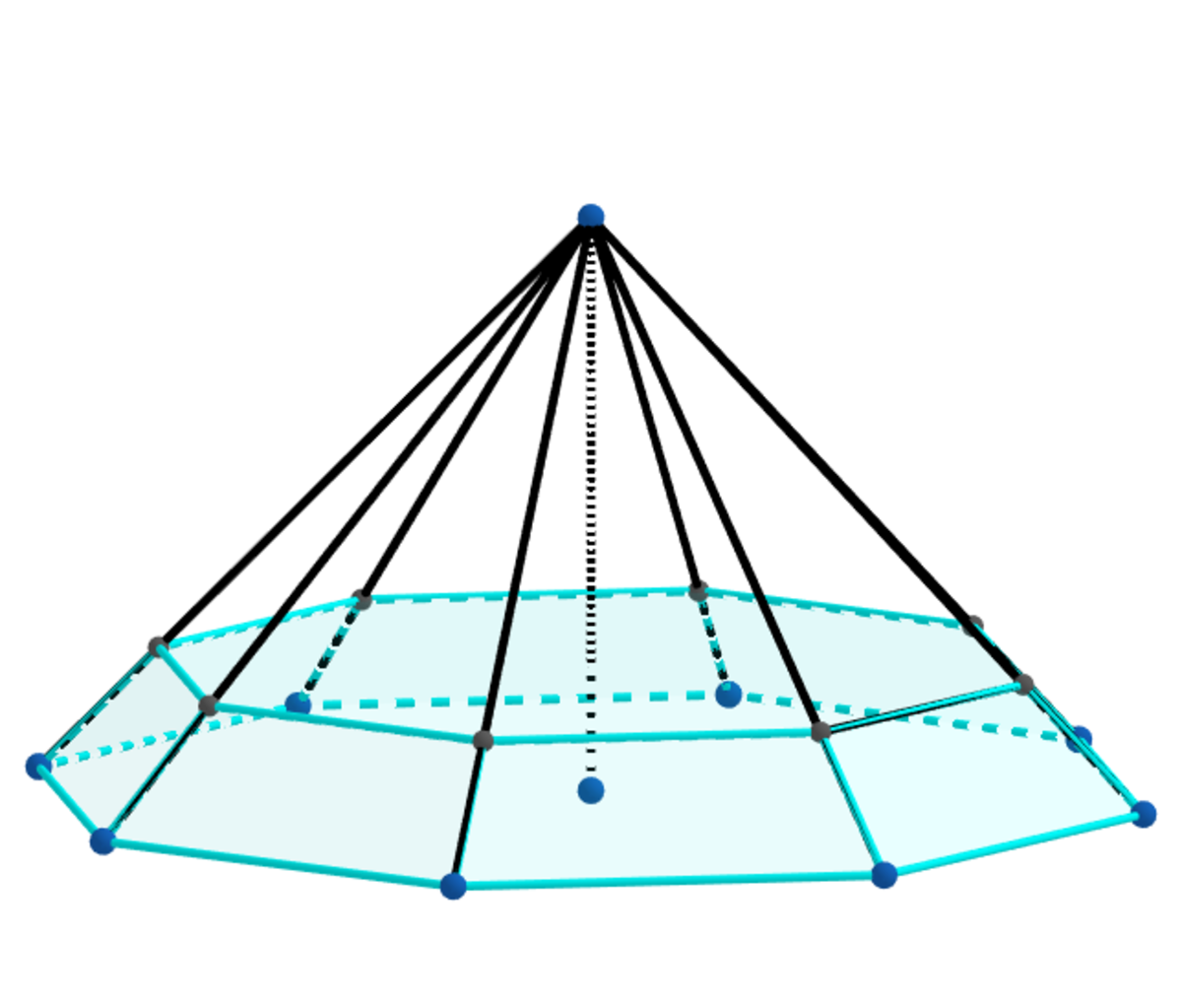
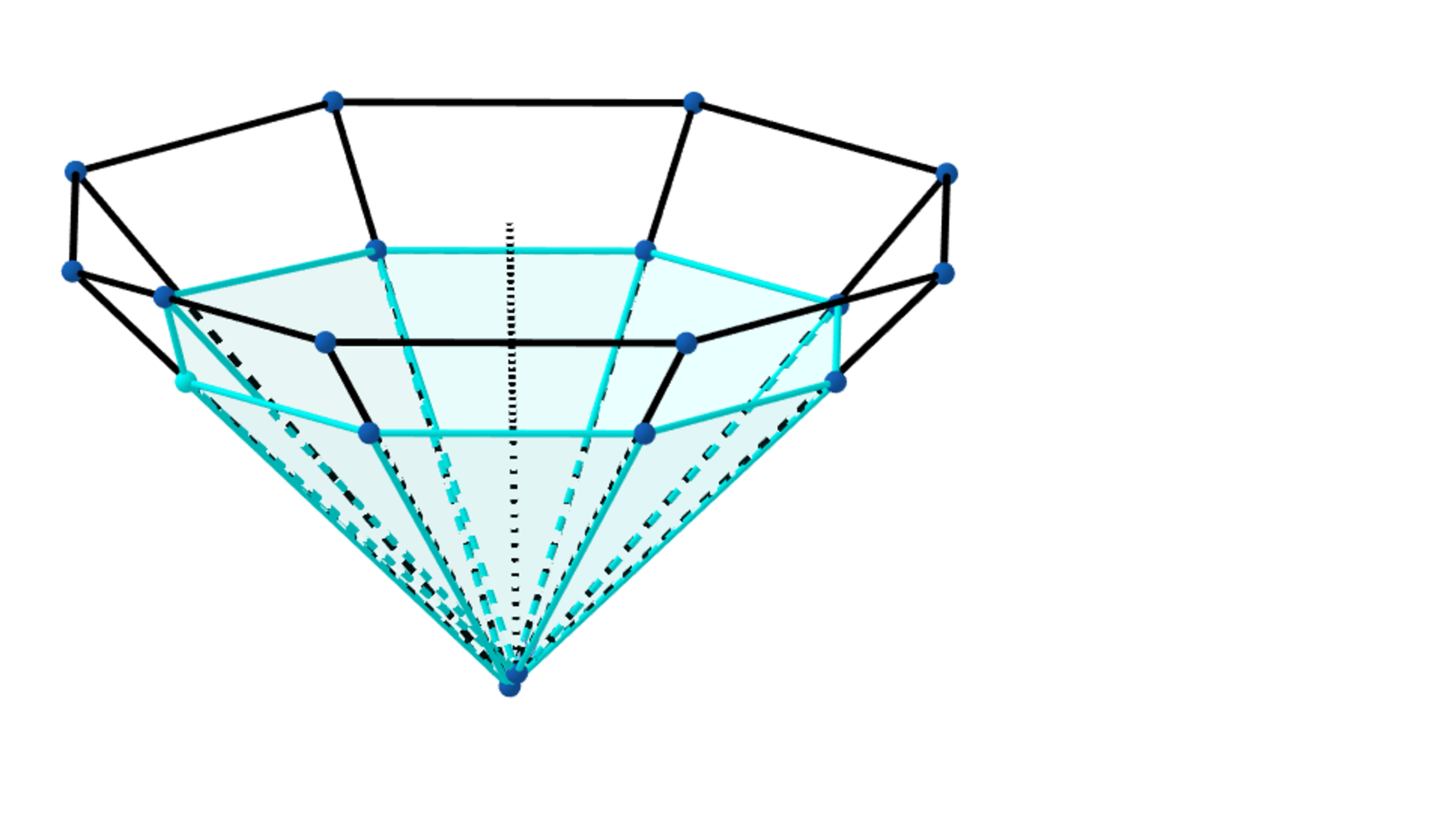
Extend the above pyramid to a - gonal pyramid.
In the first diagram the filled water is cm from the vertex of the - gonal pyramid.
In the second diagram the - gonal pyramid is turned upside down and the filled water is cm from the base of the pyramid.
What is the height of the - gonal pyramid?
The answer is 10.2195.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Clearly in both cases the volume is the same.
Let x be the length of a side of the n gon.
2 x = r sin ( n π ) ⟹ r = 2 sin ( n π ) x ⟹ h = r cos ( n π ) = 2 1 x cot ( n π ) ⟹
The area A of the n gon is A = 4 1 cot ( n π ) x 2 ⟹
The volume V of the n - gonal pyramid is V = 1 2 1 x 2 cot ( n π ) H
Let h 1 = 2 1 x 1 cot ( n π )
△ P S T ∼ △ P S R ⟹ x 1 cot ( n π ) 1 6 = x cot ( n π ) 2 H
⟹ x 1 8 = x H ⟹ x 1 = H 8 x
⟹ V 1 = 1 2 1 x 2 cot ( n π ) H − 1 2 1 ( H 8 x ) 2 cot ( n π ) ( 8 ) = 1 2 1 x 2 cot ( n π ) ( H 2 H 3 − 5 1 2 )
Let h 2 = 2 1 x 2 cot ( n π )
△ P U V ∼ △ P R Q ⟹ x 2 cot ( n π ) 2 ( H − 2 ) = x cot ( n π ) 2 H ⟹ x 2 H − 2 = x H ⟹
x 2 = H ( H − 2 ) x ⟹ V 2 = 1 2 1 ( H 2 ( H − 2 ) 2 ) x 2 cot ( n π ) ( H − 2 ) =
1 2 1 cot ( n π ) x 2 H 2 ( H − 2 ) 3
V 1 = V 2 ⟹ H 3 − 5 1 2 = H 3 − 6 H 2 + 1 2 H − 8 ⟹ H 2 − 2 H − 8 4 = 0
Taking the positive root ⟹ H = 1 + 8 5 ≈ 1 0 . 2 1 9 5