What's the length of the chord?
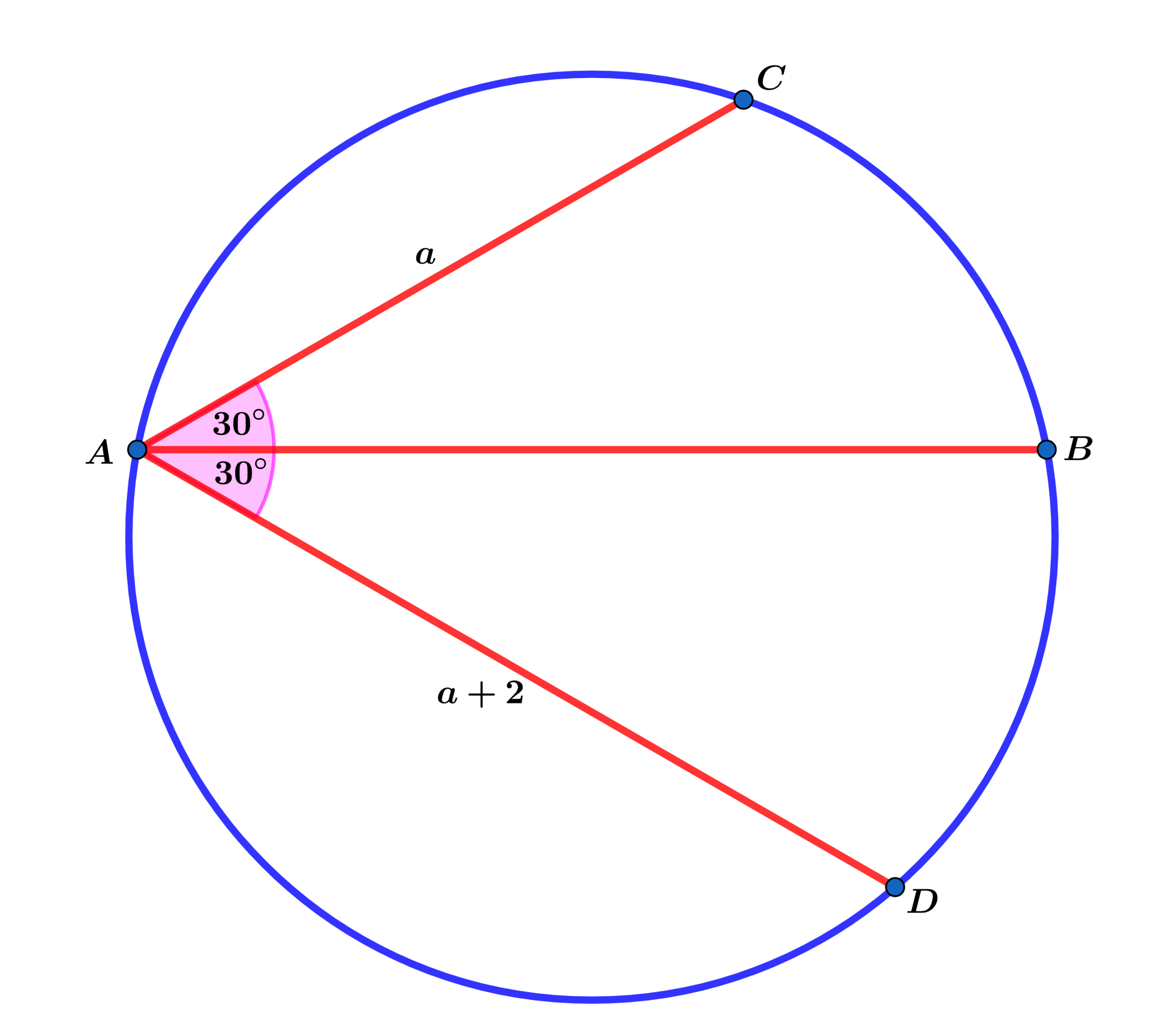
In the diagram above, the inscribed ∠ C A D has a measure of 6 0 ∘ and A B bisects ∠ C A D so that m ∠ C A B = m ∠ B A D = 3 0 ∘ and A C = a and A D = a + 2 .
Find the value of a for which A B = 6 3 .
The answer is 8.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
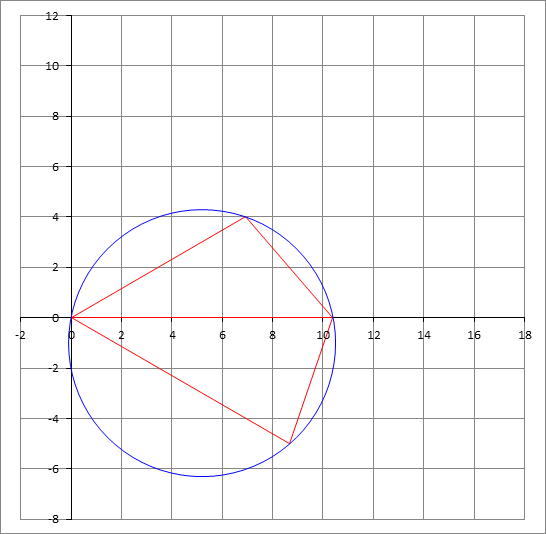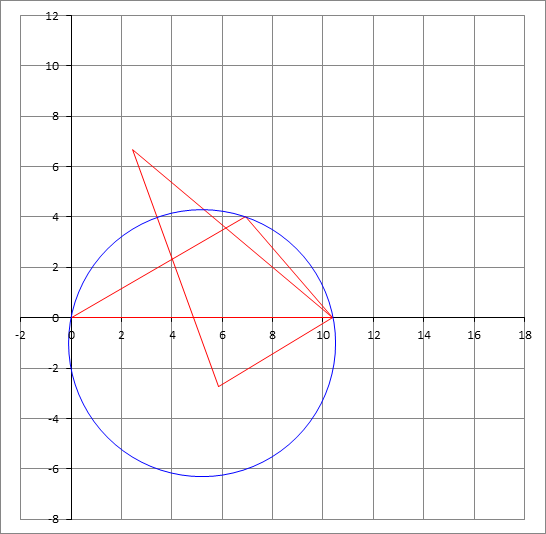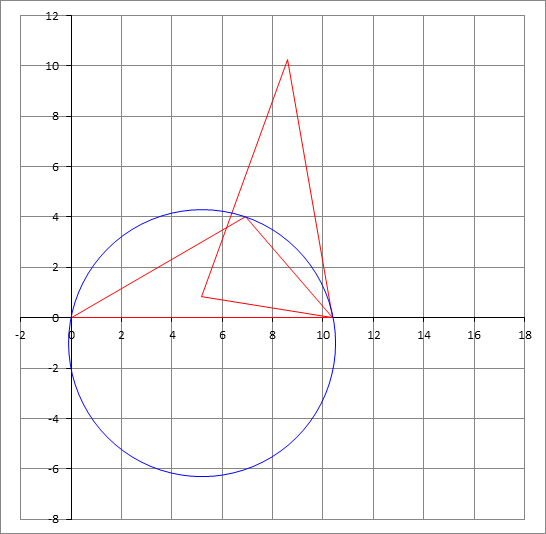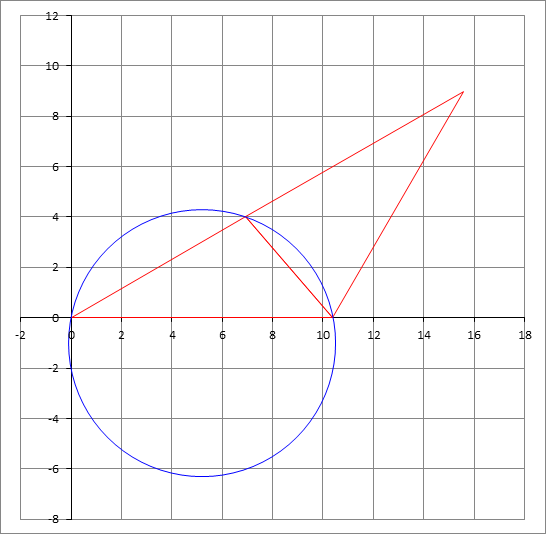
It is straight forward to find that ∠ A C B + ∠ A D B = 1 8 0 ∘ , and that B C = B D . Hence, we can rotate the lower triangle △ A B D about point B by 1 2 0 ∘ clockwise to obtain an isosceles triangle having the two equal sides = 6 3 and the base angle 3 0 ∘ . The base is a + ( a + 2 ) = 2 ( a + 1 ) , and therefore, a + 1 = 6 3 sin 6 0 ∘ = 9 , hence a = 8 .
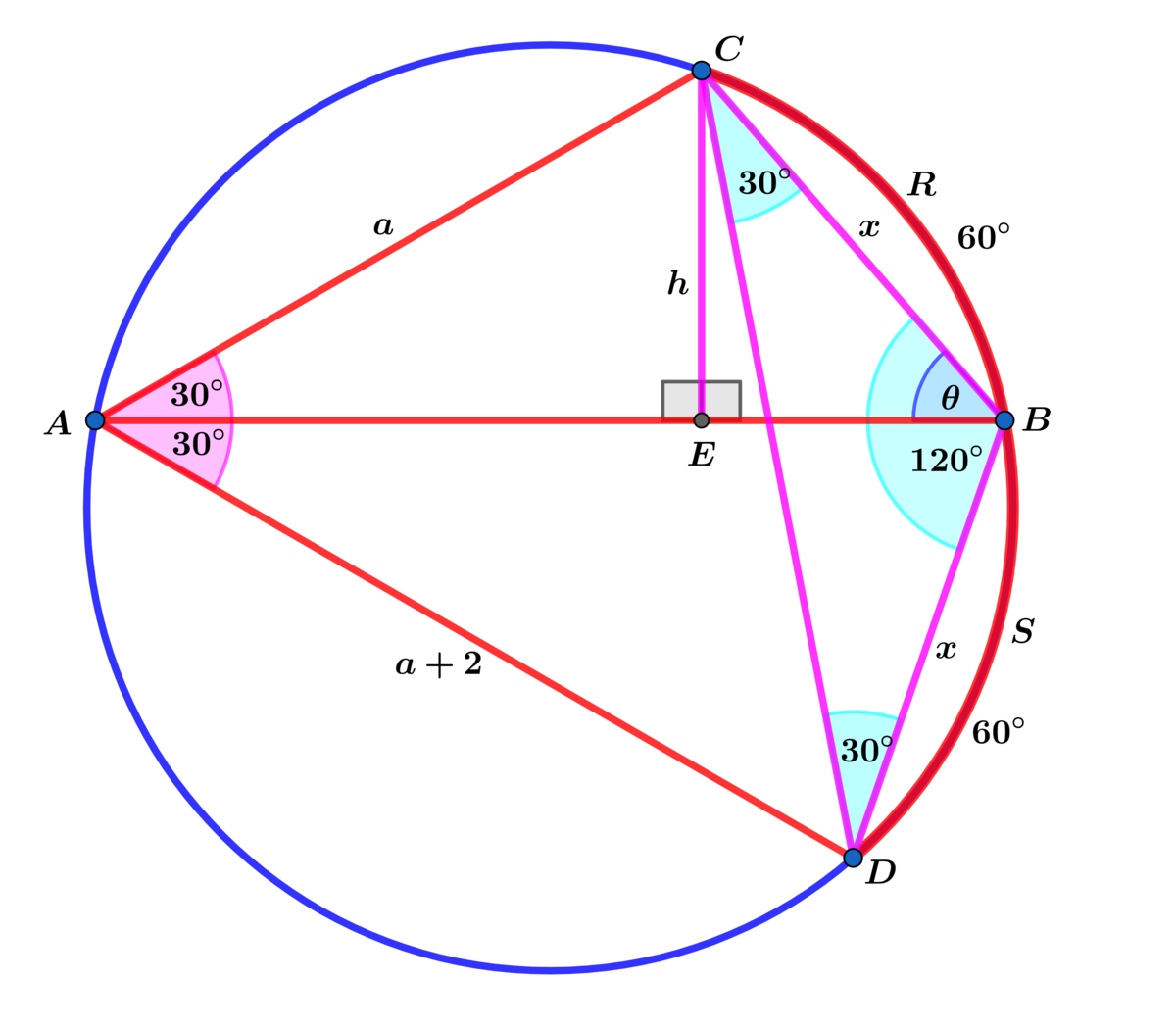
In right △ A C E : A E = a cos ( 3 0 ∘ ) = 2 3 and h = C E = 2 a
Using law of cosines on △ A C D with included ∠ C A D ⟹ C D 2 = a 2 + 2 a + 4
Using law of cosines on △ C B D with included ∠ C B D ⟹
a 2 + 2 a + 4 = 2 x 2 ( 1 + cos ( 6 0 ∘ ) ) = 3 x 2 ⟹ x = 3 a 2 + 2 a + 4
and h = 2 a = 3 a 2 + 2 a + 4 sin ( θ ) ⟹ sin ( θ ) = 2 a 3 a 2 + 2 a + 4 ⟹
cos ( θ ) = 2 a 2 + 2 a + 4 a 2 + 8 a + 1 6 ⟹ E B = 3 a 2 + 2 a + 4 cos ( θ ) =
2 3 a 2 + 8 a + 1 6 ⟹ A B = E B + A E = 2 3 1 ( a 2 + 8 a + 1 6 + 3 a ) = 6 3
⟹ a 2 + 8 a + 1 6 = 3 ( 1 2 − a ) ⟹ a 2 + 8 a + 1 6 = 1 2 9 6 − 2 1 6 a + 9 a 2 ⟹
8 ( a 2 − 2 8 a + 1 6 0 ) = 0 ⟹ ( a − 2 0 ) ( a − 8 ) = 0 and a < 1 2 ⟹ a = 8 .
Since A C B D is a cyclic quadrilateral , then ∠ B C D = ∠ B A D = 3 0 ∘ and ∠ C D B = ∠ C A B = 3 0 ∘ . And △ B C D is isosceles. Let B C = D B = b . Then D C = 2 b cos 3 0 ∘ = 3 b . By Ptolemy's theorem
A C ⋅ B D + B C ⋅ A D a b + b ( a + 2 ) a + a + 2 ⟹ a = A B ⋅ C D = 6 3 ⋅ 3 b = 1 8 = 8 Divide both sides by b