What's the length of the string?
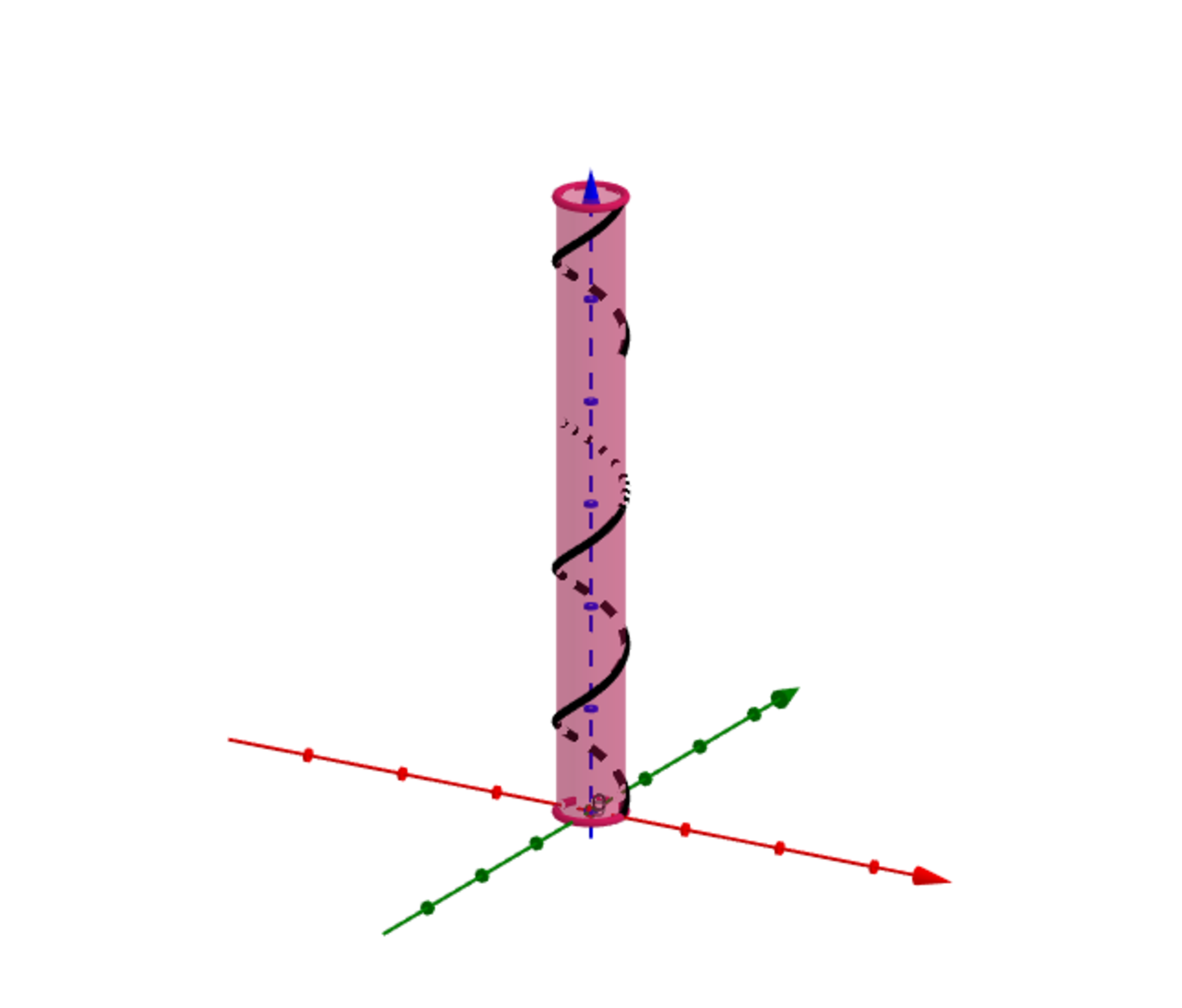
Let n be a positive integer.
A string is wound symmetrically around a circular rod. The string goes exactly n times around the rod and the rod has a circumference of n and a length of 3 n
Find the value of n for which the length of the string is 2 0 .
The answer is 4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Cool! Geometry is much easier than Calculus. But wouldn't the string be curved, so I don't understand how it would be a straight line?
Log in to reply
Nope, no curve. Just draw a straight line diagonally on a piece of paper and roll it up into a cylinder.
Log in to reply
Oh! Now that I think of it like that, it makes sense. Thank you sir! Love your solution by the way :)
I had a similar approach! Nice and clear explanation. Upvoted. :)
I think this problem is very similar to this one
Hmm... I thought Calculus was used to prove the uniqueness of the solution, but anyway, same approach:)
Let r be the radius of the rod.
2 π r = n ⟹ r = 2 π n
⟹ x = 2 π n cos ( θ ) , y = 2 π n sin ( θ ) and z = 2 π 3 θ , where θ ∈ [ 0 , 2 π n ] .
⟹ d θ d x = − 2 π n sin ( θ ) , d θ d y = 2 π n cos ( θ ) and d θ d z = 2 π 3
⟹ the length of the string L = ∫ 0 2 π n ( d θ d x ) 2 + ( d θ d y ) 2 + ( d θ d z ) 2 d θ
= ∫ 0 2 π n 2 π n 2 + 9 d θ = 2 π n 2 + 9 θ ∣ 0 2 π n = n n 2 + 9 = 2 0 ⟹
n 2 ( n 2 + 9 ) = 4 0 0 ⟹ n 4 + 9 n 2 − 4 0 0 = 0 ⟹ n 2 = 1 6 , − 2 5 ⟹ n = ± 4 , ± 5 i
∴ n = 4 .
No need calculus to solve this problem; just geometry.
Imagine that you apply ink on the string and then roll it on a piece of paper. Then the string will trace a (blue) straight line print on the paper. Since the string has traversed a horizontal distance of n × n = n 2 and a vertical distance of 3 n . The hypotenuse of the right triangle is the length of the string 2 0 . Therefore n 4 + 9 n 2 = 2 0 ⟹ n n 2 + 9 = 2 0 ⟹ n = 4 .