What's the Maximum
Let S be a sequence whose first few terms are as follows: 5 0 3 1 , 5 2 4 4 , 5 8 1 9 , 6 9 2 1 6 , … , 5 0 0 + 3 n 3 n 2 , …
The largest term of the sequence can be expressed as M N
Find the value of M − N .
The answer is 1480.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
First 10 term's are , 1/503 , 4/524 , 9/581 , 16/692 , 25/875 , 36/1148 , 49/1529 , 64/2036 , 81/2687 , 100/3500.
Here , first < second < third < forth < fifth < sixth < seventh but after seventh , 7 th > 8 th > 9 th > 10 th > ..................... etc.
For this reason , 49/1529 is the largest term of the sequence .
So , M = 1529 , N = 49 .
M-N = 1480 .
the n'th term comes out to be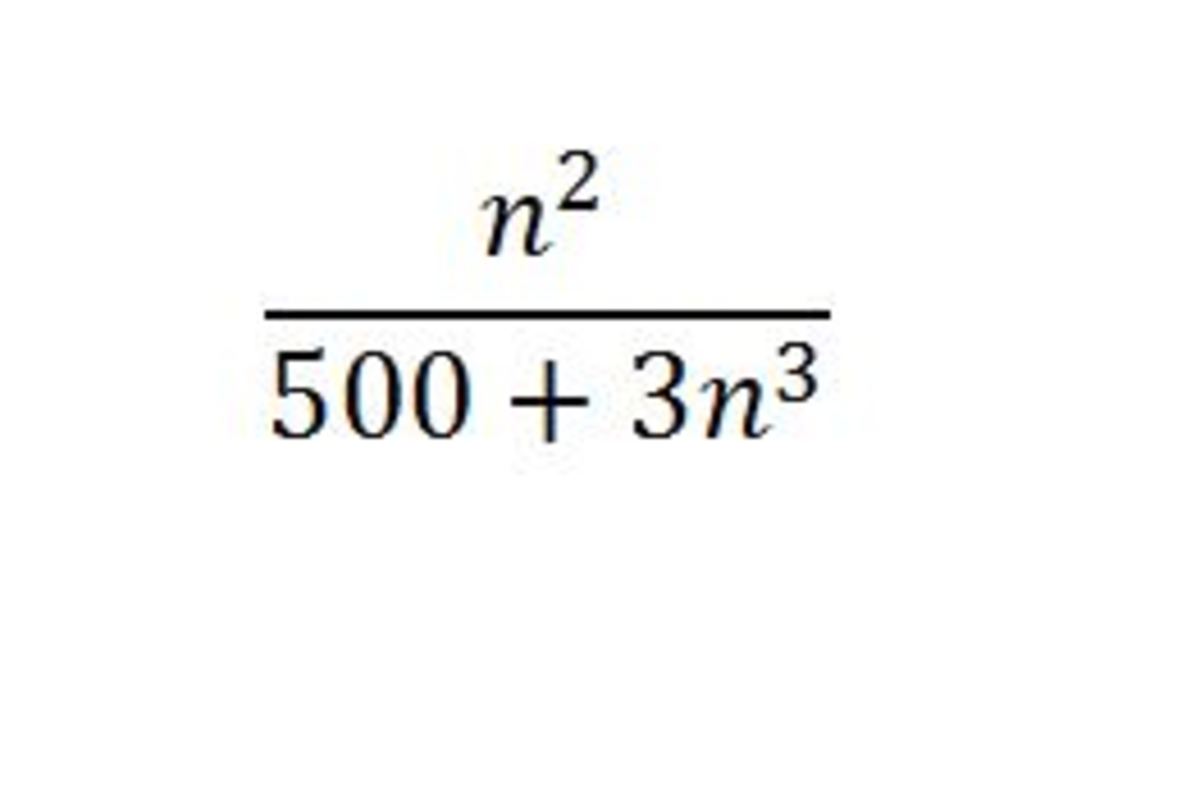 differentiate it and equate to 0 to find the point of maxima which comes out to be nearly 7
differentiate it and equate to 0 to find the point of maxima which comes out to be nearly 7
and the 7 term is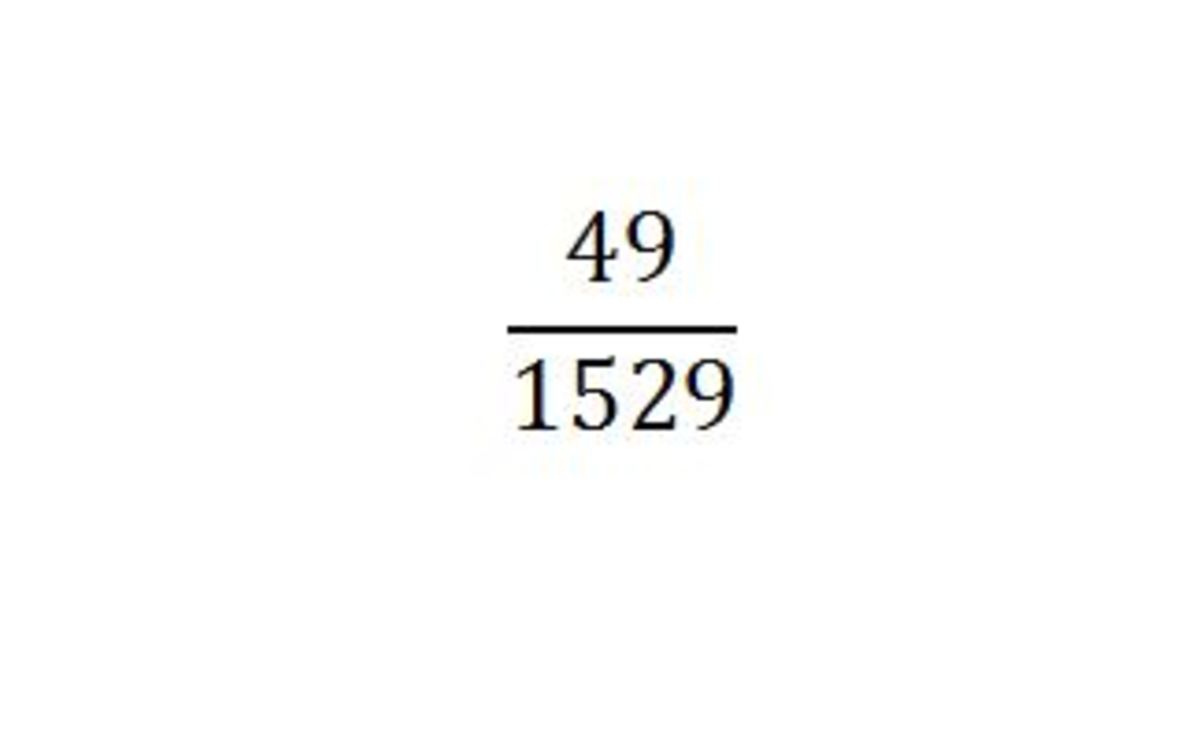
hence the difference is 1480