What's the Radius?
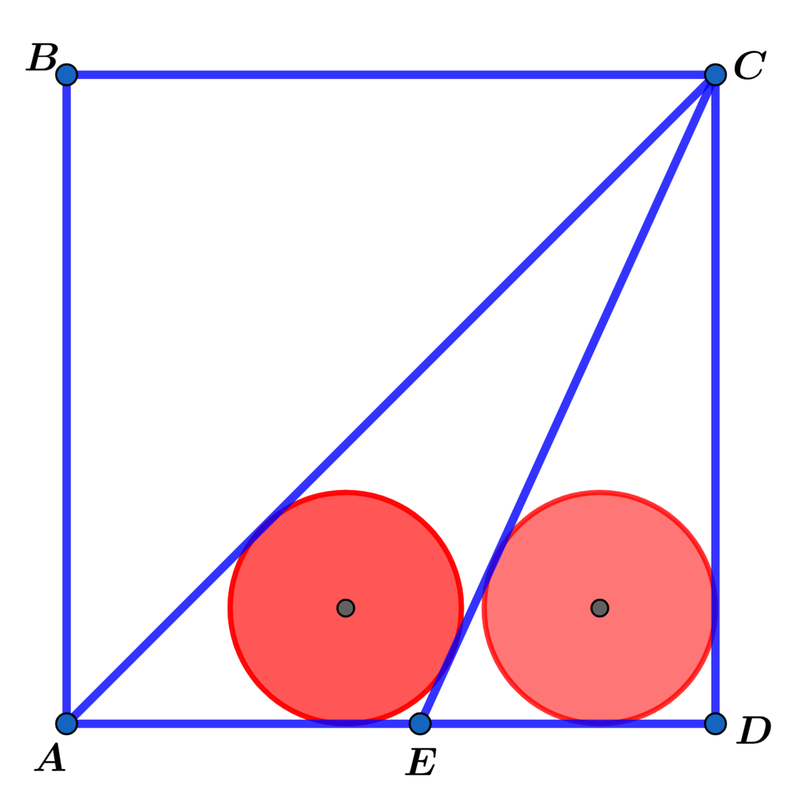
In square A B C D with side length 1 and diagonal A C and E C , the two red circles are congruent with radius r and tangent to the sides of △ A C E and △ E C D as shown above.
If the radius r can be expressed as r = ω λ − ω − λ , where λ and ω are coprime positive integers, find λ + ω .
The answer is 3.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
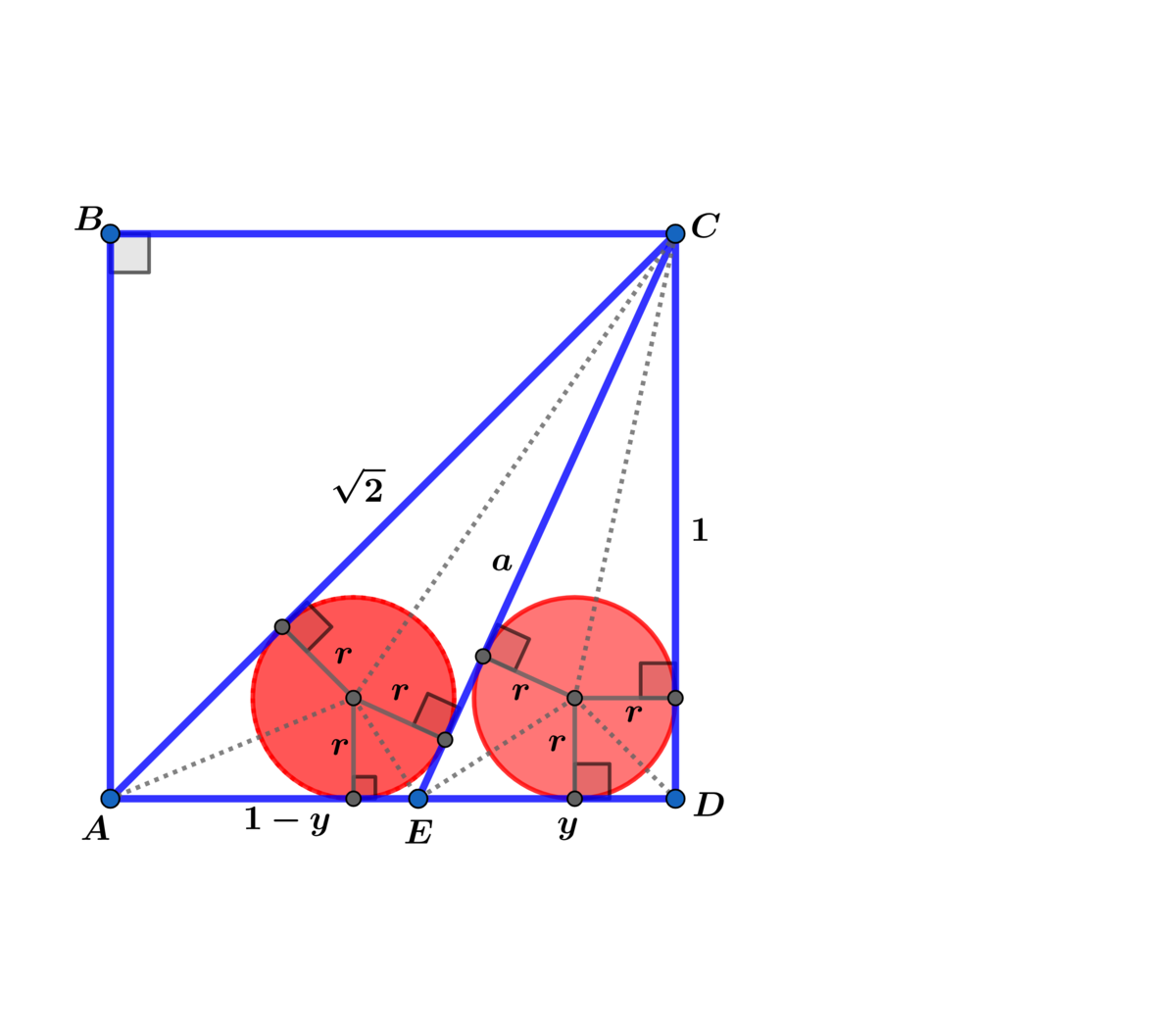
A △ E C D = 2 1 y = 2 1 r ( a + y + 1 ) ⟹ r = a + y + 1 y
and
A △ A C E = 2 1 r ( a + 2 + 1 − y ) = 2 1 ( 1 − y ) ⟹
r = a + 2 + 1 − y 1 − y = a + y + 1 y ⟹ ( 2 a + 2 + 1 ) y = a + 1 ⟹
y = 2 a + 2 + 1 a + 1
In △ E C D ⟹ y 2 + 1 = a 2 ⟹ ( a + 1 ) 2 + ( 2 a + 2 + 1 ) 2 = a 2 ( 2 a + 2 + 1 ) 2
⟹ ( a + 1 ) ( a + 1 − ( a − 1 ) ( 2 a + 2 + 1 ) 2 ) = 0 and a = 1 ⟹
2 a 3 + 2 2 a 2 − ( 2 + 1 ) a − 2 ( 2 + 1 ) = 0 ⟹
2 a 2 ( a + 2 ) − ( 2 + 1 ) ( a + 2 ) = 0 ⟹ ( 2 a 2 − ( 2 + 1 ) ) ( a + 2 ) = 0
and a = − 2 ⟹ a 2 = 2 2 + 1 ⟹ a = 2 2 + 1
⟹ y 2 + 1 = 2 2 + 1 ⟹ y = 2 2 − 1
Let α = 2 + 1 and β = 2 − 1 ⟹ a = 2 α and y = 2 β ⟹
r = a + y + 1 y = α + β + 2 β = 4 2 β ( α + β − 2 )
= 4 2 ( 1 + 2 − 1 − 2 β ) = 4 2 ( 1 − β ) =
2 1 − 2 − 1 = ω λ − ω − λ ⟹ λ + ω = 3 .
By the properties of a unit square, A D = C D = 1 and A C = 2 . Let E D = x , so that A E = A D − E D = 1 − x , and E C = E D 2 + C D 2 = x 2 + 1 .
Then the areas of △ A E C and △ E D C are A △ A E C = 2 1 ⋅ A E ⋅ C D = 2 1 ⋅ ( 1 − x ) ⋅ 1 = 2 1 ( 1 − x ) and A △ E D C = 2 1 ⋅ E D ⋅ C D = 2 1 ⋅ x ⋅ 1 = 2 1 x .
And the perimeters are P △ A E C = A E + A C + E C = 1 − x + 2 + x 2 + 1 and P △ E D C = E D + C D + E C = x + 1 + x 2 + 1 .
Since the inradius is r = P 2 A , then r = P △ A E C 2 A △ A E C = P △ E D C 2 A △ E D C , or r = 1 − x + 2 + x 2 + 1 1 − x = x + 1 + x 2 + 1 x , which solves to x = 2 1 ( 2 − 1 ) .
Substituting x = 2 1 ( 2 − 1 ) into r = x + 1 + x 2 + 1 x and solving gives r = 2 1 − 2 − 1 , so λ = 1 , ω = 2 , and λ + ω = 3 .
Let the centers of the left and right circles be O and P respectively, O M and P N be perpendicular to A D , P L is perpendicular to C D , and ∠ E C D = θ . Then ∠ C E D = 9 0 ∘ − θ and ∠ C E A = 9 0 ∘ + θ . Note that ∠ C A D = 4 5 ∘ , and C P , E P , O E , and A O bisect ∠ E C D , ∠ C E D , ∠ C E A , and ∠ C A D respectively.
We can apply half-angle tangent substitution to solve triangle incircle problems reducing them to solving polynomial equations. From
C L + L D r cot 2 θ + r t r + r ⟹ t = C D = 1 = 1 = 1 − r r Let t = tan 2 θ
From:
A M + M E + E N + N D r cot 2 2 . 5 ∘ + r cot ( 4 5 ∘ + 2 θ ) + r cot ( 4 5 ∘ − 2 θ ) + r ( 2 + 1 ) r + 1 + t 1 − t ⋅ r + 1 − t 1 + t ⋅ r + r ( 2 + 2 ) r + ( 1 − 2 r ) r + 1 − 2 r r 4 r 3 − ( 8 + 2 2 ) r 2 + ( 6 + 2 ) r − 1 ⟹ r = A D = 1 = 1 = 1 = 0 = ⎩ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎧ 1 + 2 1 2 1 − 2 − 1 2 1 + 2 − 1 Note that t = 1 − r r for r = 2 1
The acceptable value is r = 2 1 − 2 − 1 . Therefore λ + ω = 1 + 2 = 3 .