What's The Radius?
 A
=
(
4
0
0
,
1
5
5
)
,
B
=
(
6
5
0
,
5
5
0
)
,
C
=
(
3
7
0
,
6
3
6
)
.
A
=
(
4
0
0
,
1
5
5
)
,
B
=
(
6
5
0
,
5
5
0
)
,
C
=
(
3
7
0
,
6
3
6
)
.
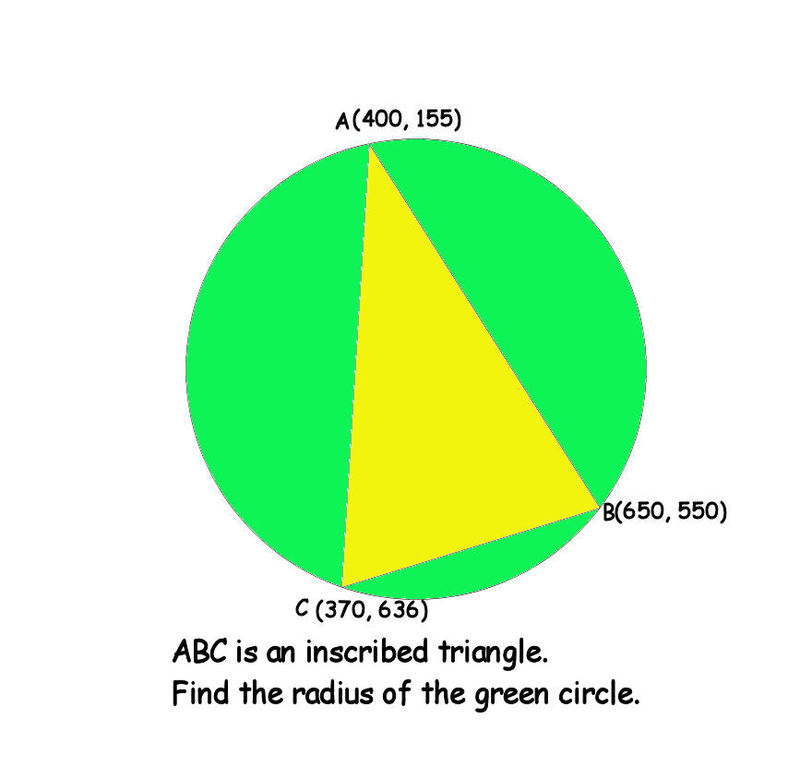
To 2 decimal places, what is the radius of the circumcircle of A B C ?
The answer is 249.77.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
I too did the same
The above solution was great (I used it), but you can use the matrix form of the area of a triangle given three coordinates to find the area. Just imput this URL and see what I mean. https://www.google.com/search?q=area+of+a+triangle+matrix&safe=strict&rlz=1C1CHBF enUS715US715&espv=2&biw=1366&bih=662&source=lnms&tbm=isch&sa=X&ved=0ahUKEwjU5KPdxoHQAhVnwYMKHe-kBVkQ AUIBigB#imgrc=rZklBWB415Q-cM%3A
Let the coordinates of the center of the circumcircle be O ( x , y ) and its radius R .
Then, we have:
⎩ ⎪ ⎨ ⎪ ⎧ R 2 R 2 R 2 = = = ( x − 4 0 0 ) 2 + ( y − 1 5 5 ) 2 ( x − 6 5 0 ) 2 + ( y − 5 5 0 ) 2 ( x − 3 7 0 ) 2 + ( y − 6 3 6 ) 2 . . . ( 1 ) . . . ( 2 ) . . . ( 3 )
⎩ ⎪ ⎨ ⎪ ⎧ R 2 R 2 R 2 = = = x 2 − 8 0 0 x + 1 6 0 0 0 0 + y 2 − 3 1 0 y + 2 4 0 2 5 x 2 − 1 3 0 0 x + 4 2 2 5 0 0 + y 2 − 1 1 0 0 y + 3 0 2 5 0 0 x 2 − 7 4 0 y + 1 3 6 9 0 0 + y 2 − 1 2 7 2 y + 4 0 4 4 9 6 . . . ( 1 ) . . . ( 2 ) . . . ( 3 )
E q . 1 − E q . 2 and E q . 3 − E q . 2 :
{ 0 0 = = 5 0 0 x − 2 6 2 5 0 0 + 7 9 0 y − 2 7 8 4 7 5 5 6 0 x − 2 8 5 6 0 0 − 1 7 2 y + 1 0 1 9 9 6 . . . ( 4 ) . . . ( 5 )
{ 5 0 0 x + 7 9 0 y 5 6 0 x − 1 7 2 y = = 5 4 0 9 7 5 1 8 3 6 0 4 . . . ( 4 ) . . . ( 5 )
E q . 4 / 7 9 0 and E q . 5 / 1 7 5 :
{ 0 . 6 3 2 9 1 1 3 9 2 x + y 3 . 2 5 5 8 1 3 9 5 3 x − y = = 6 8 4 . 7 7 8 4 8 1 1 0 6 7 . 4 6 5 1 1 6 . . . ( 6 ) . . . ( 7 )
E q . 6 + E q . 7 : 3 . 8 8 8 7 2 5 3 4 6 x = 1 7 5 2 . 2 4 3 5 9 7 ⇒ x = 4 5 0 . 5 9 5 8 7 4 3
Substituting value of x in E q . 6 : ⇒ y = 3 9 9 . 5 9 1 2 1 8 8
Substituting values of x and y in E q . 1 :
R 2 = ( 4 5 0 . 5 9 5 8 7 4 3 − 4 0 0 ) 2 + ( 3 9 9 . 5 9 1 2 1 8 8 − 1 5 5 ) 2
= ( 5 0 . 5 9 5 8 7 4 3 − 4 0 0 ) 2 + ( 2 4 4 . 5 9 1 2 1 8 8 − 1 5 5 ) 2
= 2 5 5 9 . 9 4 2 5 + 5 9 8 2 4 . 8 6 4 3
= 6 2 3 8 4 . 8 0 6 8
⇒ R = 6 2 3 8 4 . 8 0 6 8 = 2 4 9 . 7 7
We can use the extended sine rule. a/sin(A) = b/sin(B) =c/sin(C) = 2R where R is the circumradius. Since we are given the coordinates, we can use Pythagoras to find out the length of the sides. We can then use the cosine rule to find out one of the angles.
U s e m i d p o i n t a n d s l o p e f o r m u l i i f o r A B t o g e t F a n d m c . S i m i l a r l y g e t E a n d m b f o r A C . L i n e f r o m D a n d s l o p e m c − 1 , i n t e r s e c t l i n e f r o m F a n d s l o p e m b − 1 a t O . U s e l e n g t h f o r m u l a t o f i n d t h e l e n g t h o f A O = r e q u i r e d R = 2 4 9 . 7 7 .
Kudos to Sujay Motani for his really elegant solution, unlike my rather tedious solution.
Let θ = ∠ B A C and the radius be r .
By the cosine rule, cos θ = 2 × A B × A C A B 2 + A C 2 − B C 2 .
Similarly, cos 2 θ = 2 × r × r r 2 + r 2 − B C 2 = 2 r 2 2 r 2 − B C 2 .
Combining the two equations gives
2 cos − 1 ( 2 × A B × A C A B 2 + A C 2 − B C 2 ) = cos − 1 ( 2 r 2 2 r 2 − B C 2 ) .
After a bit of manipulation, we get
r = 2 − 2 cos ( 2 cos − 1 ( 2 × A B × A C A B 2 + A C 2 − B C 2 ) ) B C .
Plugging in the values of A B , A C and B C by using the distance formula d = ( x 1 − x 2 ) 2 + ( y 1 − y 2 ) 2 , we get r ≈ 2 4 9 . 7 7 .
Calculate the sides of the triangle using distance formula. and use the relation Area of triangle = (abc/4R) Area of triangle = sq root (s (s-a)(s-b)(s-c)) where s=(a+b+c)/2
a,b,c sides of triangle R is circumradius of triangle