Whats the Shaded Area?
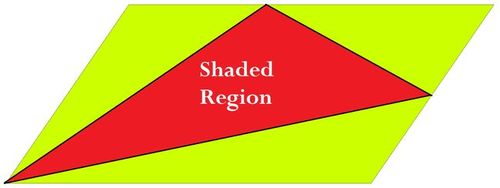
In the given parallelogram, the midpoints of two adjacent sides of the parallelogram are joined and then connected to the opposite vertex to form a triangle.
What fraction of the total parallelogram is the shaded area?
Click here for more from this set.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Given we are just dealing with a ratio of areas, we can just deform the figure into a rectangle and compute.
The Shaded Region becomes the Area of the "Rectangle" less the area of the three surrounding "Right Triangles". W ∗ H − 2 1 ( 2 W ) ( H ) − 2 1 ( W ) ( 2 H ) − 2 1 ( 2 W ) ( 2 H ) = ( W ) ( H ) ( 1 − 4 1 − 4 1 − 8 1 ) Shaded Fraction = ( W ) ( H ) ( W ) ( H ) ( 8 3 ) = 8 3
1-> Area of triangle ABE= 1/2 AE BE sin(X)= 1/2* 2 * 1 sin (X) = sin(X) sq. units 2-> Area of triangle FEC= 1/2 FC CE sin(180-X)= 1/2* 1 * 1 sin (X) = 1/2 sin(X) sq. units 3-> Area of triangle ADF= 1/2 AD DF sin(X)= 1/2* 2 * 1 sin (X) = sin(X) sq. units
4->Area of the parallelogram= product of the sides * sine of the angle b/w them =4 sin(X) sq. units
Area of the shaded region= total area- sum of areas of the triangles = (4-1-1-1/2) sin(X) sq.units =3/2 sin(X) sq. units
Area of the shaded region/Area of the parallelogram: = (3/2)/4= 3/8