This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
The limit is indeed 1 , but there is an issue with the limit as t → 0 from the left side, since for t < 0 we end up with ln ( t ) having a complex component. L'Hopital's rule does apply for complex-valued functions under certain conditions, so care would have to be taken to be sure that these conditions are met in this case.
Without applying L'Hopital's Rule, so we have: p 1 = t ⇔ t 1 = p , t , p ∈ ℜ +
e x p ( − lim p → + ∞ p lo g p ) = e x p ( 0 ) = 1
because the exponential grows faster than any power exponent.
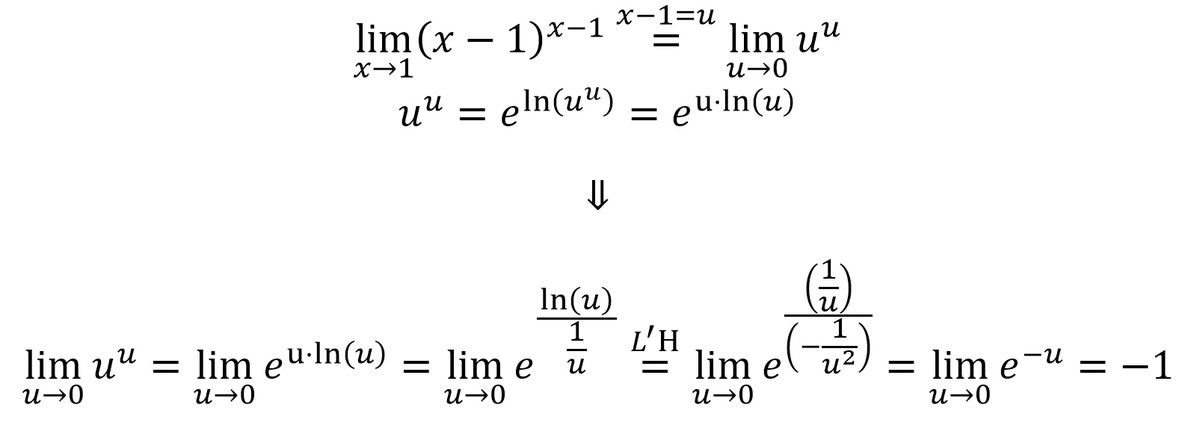
Let t = x − 1 , so we have: x → 1 lim ( x − 1 ) x − 1 = t → 0 lim t t
Using the fact that a b = exp ( b lo g a ) , we have: t → 0 lim exp ( t lo g t )
Since exp is continuous function, we can factor it out limit: exp ( t → 0 lim t lo g t ) = exp ( t → 0 lim t 1 lo g t )
Apply L'Hopital's Rule, we have: exp ( t → 0 lim − t ) = exp ( 0 ) = 1