What's the speed after moving down the inclined plane?

Classical Mechanics Level 2

A body starts moving downwards (from rest) from the upper point of an inclined plane ( A A ). What is the formula of the velocity when the object arrives at the base of the plane ( B B )?

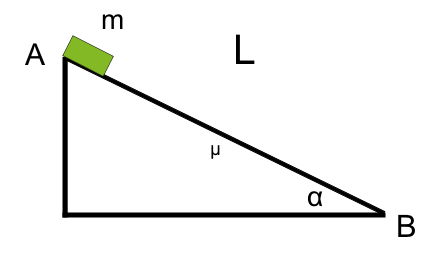
Details:

The velocity should be expressed in terms of:

  • The length of the inclined plane, L L .

  • Its angle, α \alpha .

  • The coefficient of friction on the plane, μ \mu .

  • The gravitational acceleration, g g .

v B = 2 l g ( sin ⁡ α − μ cos ⁡ α ) v_B=\sqrt{2lg(\sin\alpha-\mu\cos\alpha)} v B = 2 g h v_B=\sqrt{2gh} v B = l g ( sin ⁡ α − cos ⁡ α ) v_B=\sqrt{lg(\sin\alpha-\cos\alpha)} v B = ( l g ( sin ⁡ α − cos ⁡ α ) ) 2 v_B=(lg(\sin\alpha-\cos\alpha))^2

Victor Dumbrava by Victor Dumbrava , 17, Romania

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Victor Dumbrava
Sep 24, 2017

At the very top of the plane, the object has no initial velocity, hence its energy is equal to its potential energy:

E A = P E A = m g l sin ⁡ α E_A=PE_A=mgl\sin\alpha

The friction force acts on the body as well, and the formula is:

F f = μ m g cos ⁡ α F_f=\mu mg\cos\alpha

The work of the friction force is:

W F f = − L ⋅ F f = − L μ m g cos ⁡ α W_{F_f}=-L\cdot F_f=-L\mu mg\cos\alpha

Applying the law of mechanical energy conservation:

E B = E A + W F f E_B=E_A+W_{F_f}

E B = m g L sin ⁡ α − L μ m g cos ⁡ α E_B=mgL\sin\alpha-L\mu mg\cos\alpha

Also note that at point B B , the object has no potential energy, hence:

E B = K E B = m v B 2 2 E_B=KE_B=\frac{mv_{B}^2}{2}

m v B 2 2 = m g L ( sin ⁡ α − μ cos ⁡ α ) \frac{mv_{B}^2}{2}=mgL(\sin\alpha-\mu \cos\alpha)

v B 2 2 = g L ( sin ⁡ α − μ cos ⁡ α ) \frac{v_{B}^2}{2}=gL(\sin\alpha-\mu \cos\alpha)

⟹ v B 2 = 2 g L ( sin ⁡ α − μ cos ⁡ α ) \implies v_{B}^2=2gL(\sin\alpha-\mu \cos\alpha)

v B = 2 L g ( sin ⁡ α − μ cos ⁡ α ) \boxed{v_{B}=\sqrt{2Lg(\sin\alpha-\mu \cos\alpha)}}

2 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...