What's the Value?
Let m > 1 .
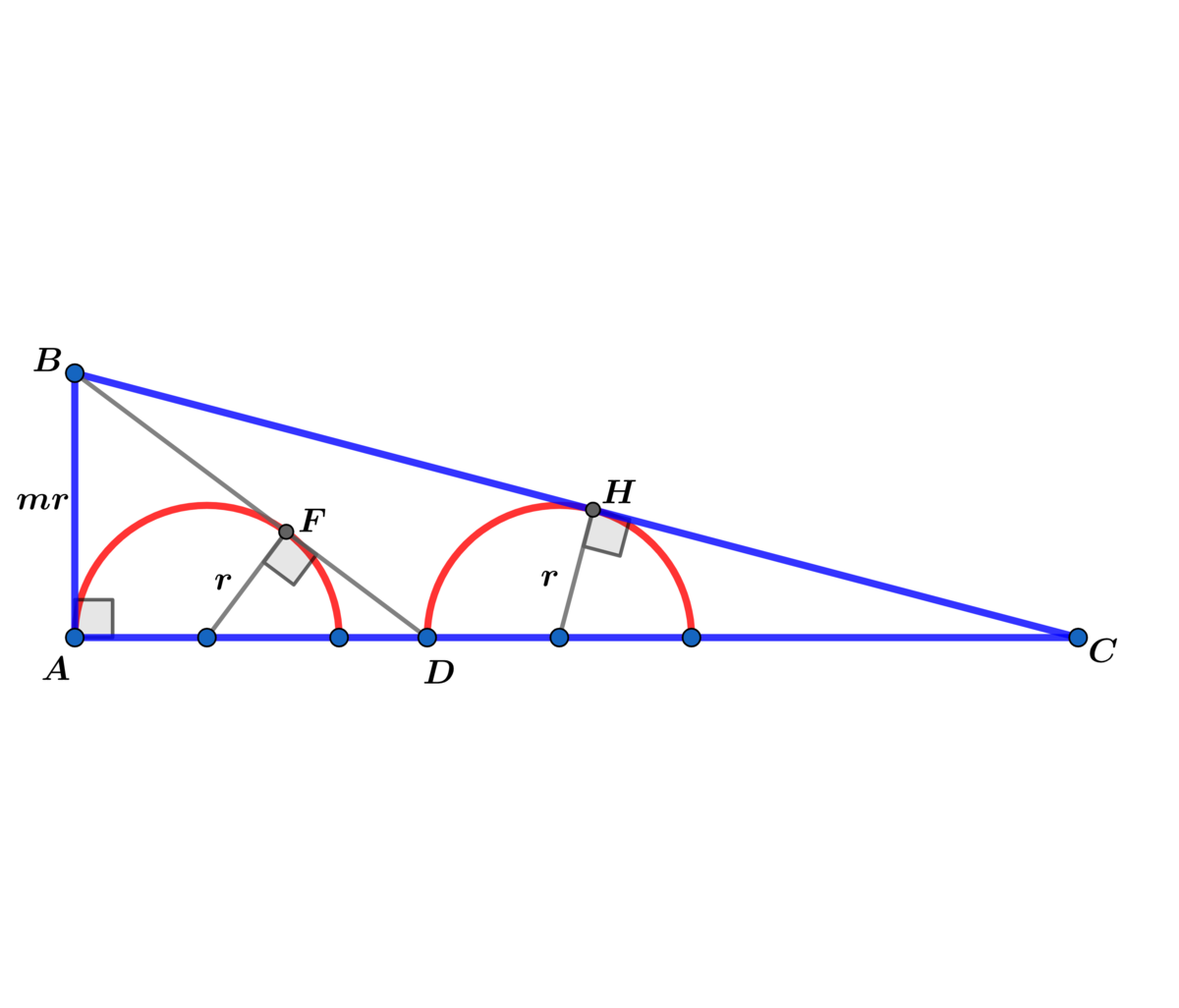
In right △ A B C with A B = m r , B D and B C are tangent to the two inscribed semicircles with radius r at F and H respectively.
If the value of m for which r A C = ( m 2 − 1 ) 2 5 m 2 can be expressed as m = d a b − c , where a , b , c and d are coprime positive integers, find a + b + c + d .
The answer is 156.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Shouldn't it be m = d a b − c instead of m = d a b + c ?
Log in to reply
Yes, it's a typing error. In my solution I used m = 4 2 2 1 − 1 2 9 , but in the problem I typed + .
△ A B D ∼ △ E F D ⟹ m = y B D ⟹ B D = m y
Using the Pythagorean theorem on △ A B D ⟹ m 2 y 2 = m 2 r 2 + ( r + y ) 2 ⟹
( m 2 − 1 ) y 2 − 2 r y − ( m 2 + 1 ) r 2 = 0 ⟹ y = m 2 − 1 m 2 + 1 r ⟹
A D = m 2 − 1 2 m 2 r ⟹ A G = A D + r = m 2 − 1 3 m 2 − 1 r
△ A B C ∼ △ G H C ⟹ m = x B C ⟹ B C = m x
Using the Pythagorean theorem on △ A B C ⟹ m 2 x 2 = m 2 r 2 + ( m 2 − 1 3 m 2 − 1 r + x ) 2
⟹ ( m 2 − 1 ) 3 x 2 − 2 ( 3 m 2 − 1 ) ( m 2 − 1 ) r x − ( ( 3 m 2 − 1 ) 2 + m 2 ( m 2 − 1 ) 2 ) r 2 = 0 ⟹
x = ( m 2 − 1 ) 2 3 m 2 − 1 + m 2 m 4 + 6 m 2 − 3 r dropping the negative root
⟹ A C = A G + x = ( m 2 − 1 ) 2 3 m 2 − 1 + m 4 + 6 m 2 − 3 m 2 r
⟹ r A C = ( m 2 − 1 ) 2 3 m 2 − 1 + m 4 + 6 m 2 − 3 m 2 = ( m 2 − 1 ) 2 5 m 2
⟹ ( ∗ ) 3 m 2 − 1 + m 4 + 6 m 2 − 3 = 5 ⟹ m 4 + 6 m 2 − 3 = 3 6 − 3 6 m 2 + 9 m 4
⟹
8 m 2 − 4 2 m 2 + 3 9 = 0 ⟹ m 1 = 4 2 2 1 − 1 2 9 and m 2 = 4 2 2 1 + 1 2 9
dropping the negative roots and since m 1 > 1 satisfies ( ∗ ) ⟹
m = 4 2 2 1 − 1 2 9 = d a b − c ⟹
a + b + c + d = 1 5 6 .
Notice letting d ( m ) = r A C ⟹ lim m → ∞ d ( m ) =
lim m → ∞ m 2 ( 1 − m 2 2 + m 4 1 ) 3 m 2 − 1 + m 4 + 6 m 2 − 3 =
lim m → ∞ 1 − m 2 2 + m 4 1 3 − m 2 1 + 1 + m 2 6 − m 4 3 = 1 4 = 4