What's with these logs?

$\ln\left(2x^{2} - 3x + 8\right) \le \dfrac{\ln\left(x^{4}+4x^{3} + 8x^{2} + 8x + 4\right)}{2}$
$\ln\left(2x^{2} - 3x + 8\right) \le \dfrac{\ln\left(x^{2}+2x+2\right)^{2}}{2}$
The determinants of both the quadratics are negative, and the leading co-efficient is greater than 0, thus they are always greater than 0, and the logarithmic function is well defined.
$\ln\left(2x^{2} - 3x + 8\right) \le\ln\left(x^{2}+2x+2\right)$
$\therefore 2x^{2} - 3x + 8 \le x^{2} + 2x + 2$
$x^{2} - 5x + 6 \le 0$
$(x-2)(x-3) \le 0$

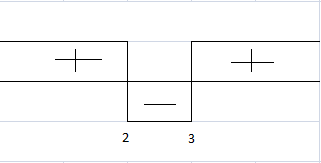
Drawing the wavy curve we get our interval as,
$x \in [2,3]$
The only integer values that satisfy this are $2,3$
$2\cdot 3 = 6$
Pardon my weirdly drawn wavy curve.