What's Your Plate Capacity?

Electricity and Magnetism Level 3

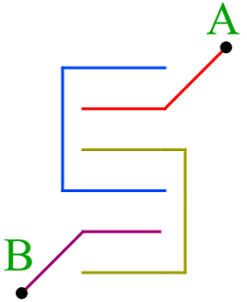
Plates are arranged as shown in the figure such that the effective area between each of them is $A$ and the effective distance between each pair of neighboring plates is $d$ . What is the net capacitance between the terminals A and B ?

Clarification : $\epsilon_0$ is the permittivity of free space.

\frac{\epsilon _0A}{d}

\frac{3\epsilon _0A}{d}

\frac{5\epsilon _0A}{2d}

\frac{7\epsilon _0A}{6d}

\frac{5\epsilon _0A}{d}

\frac{6\epsilon _0A}{d}

None of these choices

1 solution

Sparsh Sarode
Jun 5, 2016

The given plates can be taken as a set of capacitors and arranged as shown above

The points $\color{#3D99F6}{1, 2}$ and $\color{#3D99F6}{3, 4}$ are at same potential. Hence the the circuit becomes as follows:

The above circuit represents a Wheatstone bridge. Hence the capacitor marked as $\color{#D61F06} C$ becomes $\color{blueviolet}{ \text{ineffective}}$ .

$\therefore$ The net capacitance, $C_{eff}$ is

$C_{eff}=(C+C)||(C+C)=\dfrac{2C}{2}=C$ where $C=\dfrac{\epsilon _0A}{d}$

$\color{#20A900}{\boxed{ \therefore C=\dfrac{\epsilon _0A}{d}}}$

Thanks...very clear

Rishi K - 5 years ago

Welcome :)

Sparsh Sarode - 5 years ago

What's Your Plate Capacity?

1 solution

0 pending reports