Wheee!
Two identical twins, Amy and Beatrice, are on top of two different slides, one on each slide. Both slides start 3 m above the ground and end 0.5 m above the ground. Amy's slide is a straight, 45 degree slide with height given by (so it starts at with a height of three meters and ends at with a height of half a meter). Beatrice's slide is curved and the height is given by (so it starts at and ends at ). Both slides are frictionless.
If both twins start from rest at the top of their slides, what is the ratio of Amy's speed to Beatrice's speed at the bottom of the slides? i.e., what is ?
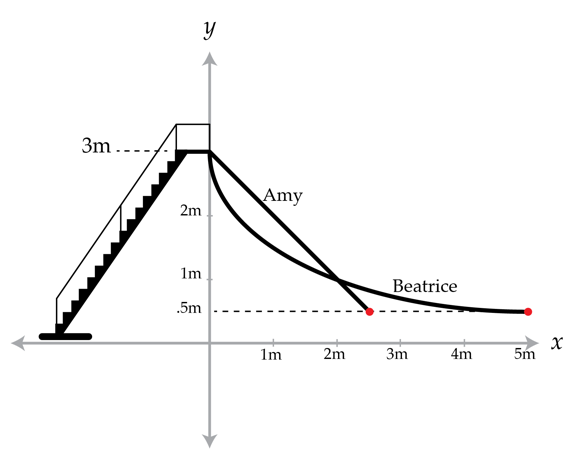
The answer is 1.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The height of each slide is the same and the stopping point is the same. Since all forces are conservative, the length of the slide doesn't matter. Conservation of energy then yields that the kinetic energy of Amy and Beatrice must be the same. Since they are identical twins, their masses are the same and hence so are their speeds.