When Hyperbola meets ellipse

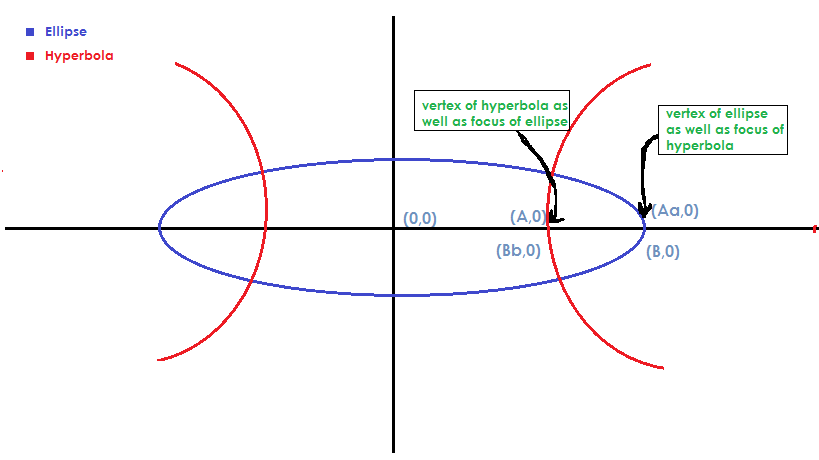
The distance from the center of an ellipse to its foci (call it $A$ ) divided by the distance to its vertices (call it $B$ ) is its eccentricity: $\frac{A}{B} .$

The distance from the center of an hyperbola to its foci (call it $C)$ divided by the distance to its vertices (call it $D)$ is its eccentricity: $\frac{C}{D} .$

We are given in the problem that $A = D$ and $B=C .$

So $\left( \frac{A}{B}\right) \left( \frac{C}{D}\right) = \left( \frac{A}{B}\right) \left( \frac{B}{A}\right) = 1 .$

Let the eccentricity of hyperbola and ellipse be a and b respectively. Let the length of transverse axis of hyperbola be A and the length of semi major axis of ellipse be B . Centre of both ellipse and hyperbola is (0,0). The transverse axis of hyperbola and the major axis of hyperbola both coincide with the x-axis. By comparing the coordinates of identical points, we obtain $\begin{aligned} Aa =B \\ a= \frac{B}{A} \\ Bb =A \\ b = \frac{A}{B} \\ \end{aligned}$ Hence we conclude that, $\begin{aligned} a \times b &=1 \end{aligned}$