Anti-Pythagoras
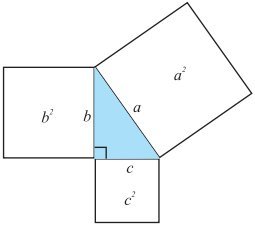
In a picture such as a triangle above, we know that the areas c 2 + b 2 = a 2 .
However, imagine a triangle with non-zero area and sides a , b , c where c is the longest , with squares extended outwards from each side, each with a side length of that triangle. In what cases is the sum of the perimeters of the squares a and b greater than the perimeter of square c ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
This is exactly how I intended it to be solved. Great solution
The sum of the perimeters of squares a and b would be P a b = 4 a + 4 b . From the law of cosines, c = a 2 + b 2 − 2 a b cos C , so the perimeter of square c would be P c = 4 a 2 + b 2 − 2 a b cos C . We were given that c is the longest side, so 6 0 ° < C < 1 8 0 ° , which means 2 1 < cos C < − 1 , so P c < 4 a 2 + b 2 − 2 a b ( − 1 ) which simplifies to P c < 4 a + 4 b . Therefore, P a b = 4 a + 4 b > P c , so the sum of the perimeters of squares a and b is always greater than the perimeter of square c .
Nice way around it which I hadn't contemplated, although it's quite calculation heavy and there are simpler ways. E.g. see @Blan Morrison solution
Relevant wiki: Triangle Inequality
The perimeter of any square, where the side length is s , is always 4 s . Therefore, we can restate the problem using an inequality:
If we divide both sides of the inequality by 4, then we get a + b > c . Most (if not all) geometry students should know this inequality as the Triangle Inequality Theorem, which states that the sum of any two sides of any triangle is always greater than the third side.
Since a + b > c is always true, then 4 a + 4 b > 4 c is always true .