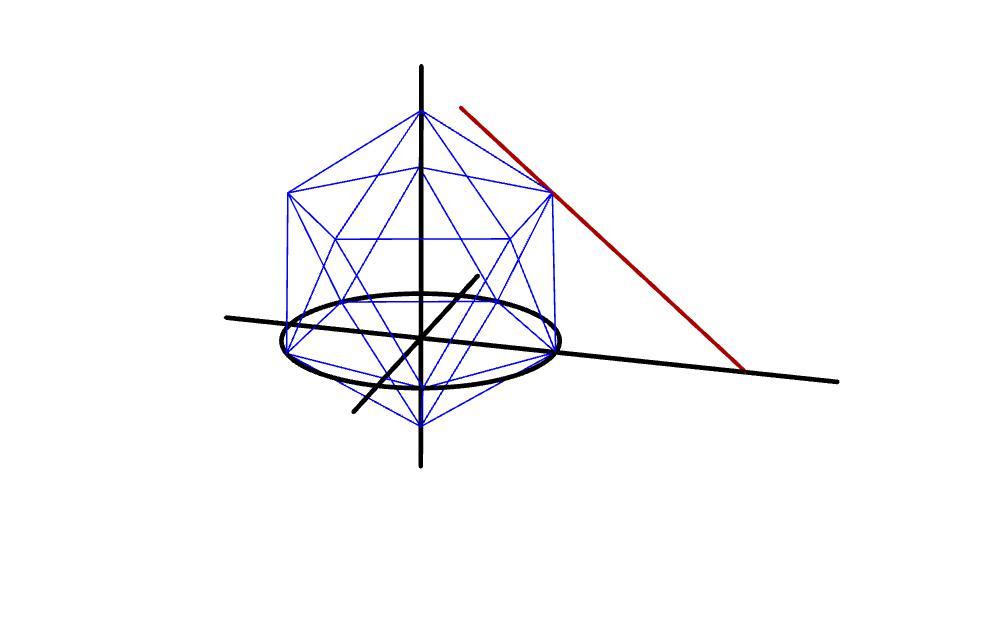
Where Line Meets Regular Icosahedron

Geometry Level 4

A circle of radius 2 on the $xy$ -plane centered at $(0, 0)$ has a regular pentagon inscribed inside it, not necessarily oriented as shown. This pentagon defines a regular icosahedron . From one of its vertices a line with a vector direction $(3, -1, -2)$ intersects the $x$ -axis at $\left(3+\sqrt{3}, 0, 0\right)$ . The coordinates of this vertex is $(x, y, z)$ .

The sum $x+y+z$ can be expressed as

$\dfrac{a+\sqrt{b}}{c} ,$

where $a, b, c$ are integers and $b$ is square-free. Find $a+b+c$ .

Note See also Regular Icosahedron for more details. Given a regular pentagon, it defines a regular icosahedron in that both the regular pentagon and the regular icosahedron share the same $5$ vertices. This would be possible with one unique regular icosahedron on either side of the plane of the regular pentagon.

The answer is 7.

1 solution

Michael Mendrin
Jan 21, 2017

From the point $\left(3+\sqrt{3}, 0, 0\right)$ , all points on the line with the vector direction of $\left(3, -1, -2\right)$ can be expressed with the following parametric equations, with $t$ as the parameter

$x=3+\sqrt{3}+3t$
$y=0-t$
$z=0-2t$

The sum $x+y+z$ is $3+\sqrt{3}$ , so the answer is $3+3+1=7$ . All this talk about the icosahedron is just a diversion.

One can rotate the icosahedron as shown by $24$ degrees counter-clockwise, then the vertex as shown will have the coordinates $\left( \sqrt{3}, 1, 2 \right)$ , which has the sum $3+\sqrt{3}$ . Adding the vectors $\left( \sqrt{3}, 1, 2\right)$ and $\left( 3, -1, -2 \right)$ will produce the point on the $x$ -axis, $\left( 3+\sqrt{3}, 0, 0 \right)$ .

Courtesy Archit Agrawal for his solution in Where Line Meets Plane and author Stephen Chase and Brian Charlesworth for inspiration.

Where Line Meets Regular Icosahedron

The answer is 7.

1 solution

0 pending reports