Are you too tired to chase angles?
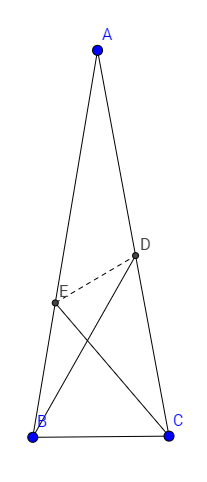 Let ABC be an isosceles triangle
with
. Point
is on
side
such that
. Point
is on side
such that
. Find the measure of
in degrees.
Let ABC be an isosceles triangle
with
. Point
is on
side
such that
. Point
is on side
such that
. Find the measure of
in degrees.
The answer is 30.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Construct a line parallel to B C through D and call its intersection with A B , F . Connect F C and call its intersection with B D , G . Since △ A B C is isosceles and ∠ D B C = 6 0 ∘ , we know that △ B G C and △ F D G are equilateral triangles.Also notice that ∠ B E C = 5 0 ∘ which implies △ B E C is B-isosceles. Since △ B G C is equilateral, this implies that B E = B C = B G which implies that △ B E G is isosceles which implies that ∠ B G E = 8 0 ∘ . Due to supplementary angles, we find that ∠ F G E = 4 0 ∘ . Also notice that ∠ B F C = 4 0 ∘ which implies that △ E F G is isosceles which implies that F E G D is a kite which gives us an answer of 3 0 ∘ since the diagonals are perpendicular.