When the sky reaches the ground
If is a real number chosen between the interval , and being positive integers , find the probability that satisfies the equation above.
Notations : denotes the floor function and denotes the ceiling function .
The answer is 0.6.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Relevant wiki: Geometric Probability
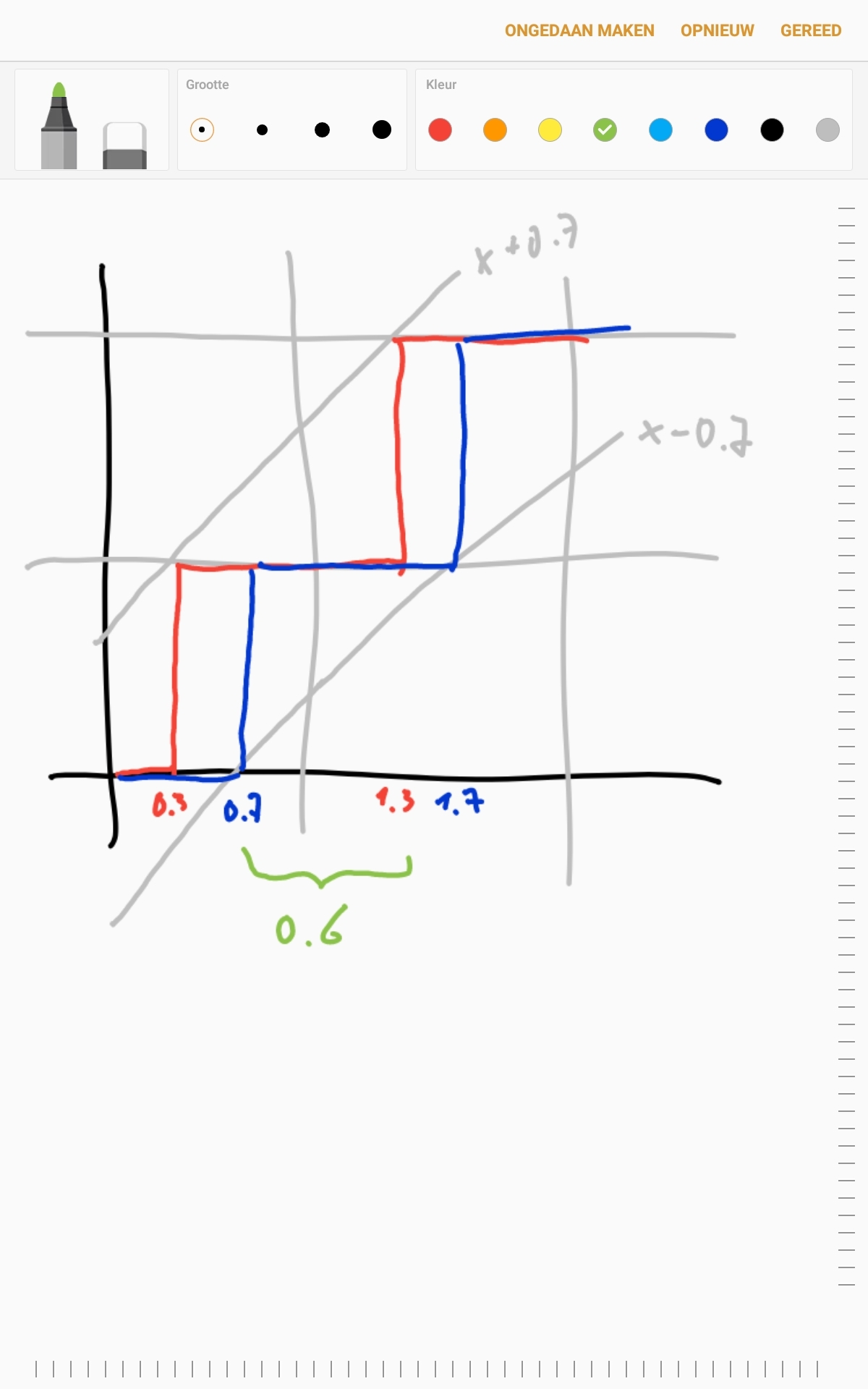
⌊ x + 0 . 7 ⌋ = ⌈ x − 0 . 7 ⌉
The range of values allowing the equation to be true is the same between every consecutive integer. Thus, regardless of the values of a and b , the odds will be the same.
For number x , we denote [ x ] as its whole part and { x } as its fractional part.
Case 1: x = x
When does ⌊ x + 0 . 7 ⌋ = x ?
That is when { x } + 0 . 7 < 1 , or { x } < 0 . 3 .
That would give us ⌊ [ x ] + w ⌋ with w = { x } + 0 . 7 , so w < 1 . This means that ⌊ [ x ] + w = x .
So if we have { x } < 0 . 3 , The RHS, on the other hand, would result to ⌈ [ x − 1 ] + z ⌉ with z < 1 . So ultimately that will give us [ x − 1 ] + 1 = x . This now validates the case.
Subsequently, if { x } > 0 . 3 , that would result to ⌊ [ x ] + y ⌋ with y > 1 , and that will give us [ x ] + 1 . This will mean that the LHS is x + 1 , while the RHS may be x , or also x + 1 , depending on { x } .
Case 2: x + 1 = x + 1
We already know that ⌊ x + 0 . 7 ⌋ = x + 1 when { x } > 0 . 3 .
So when does ⌈ x − 0 . 7 ⌉ = x + 1 ?
That is when { x } − 0 . 7 > 0 , or { x } > 0 . 7 . In this case, that would give us ⌈ [ x ] + v ⌉ , with v = { x } − 0 . 7 . That would provide a fractional part to the expression resulting it to [ x ] + 1 . Thus, this case is validated.
So, for any two consecutive integers a and a + 1 , the mentioned equation holds when { x } < 0 . 3 or { x } > 0 . 7 . So the range of permissible values is [ a , a + 0 . 3 ) ∪ ( a + 0 . 7 , a + 1 ] .
So the probability for any interval ( a , b ) would be
b − a 0 . 6 ( b − a ) = 0 . 6