When will the holidays come 2

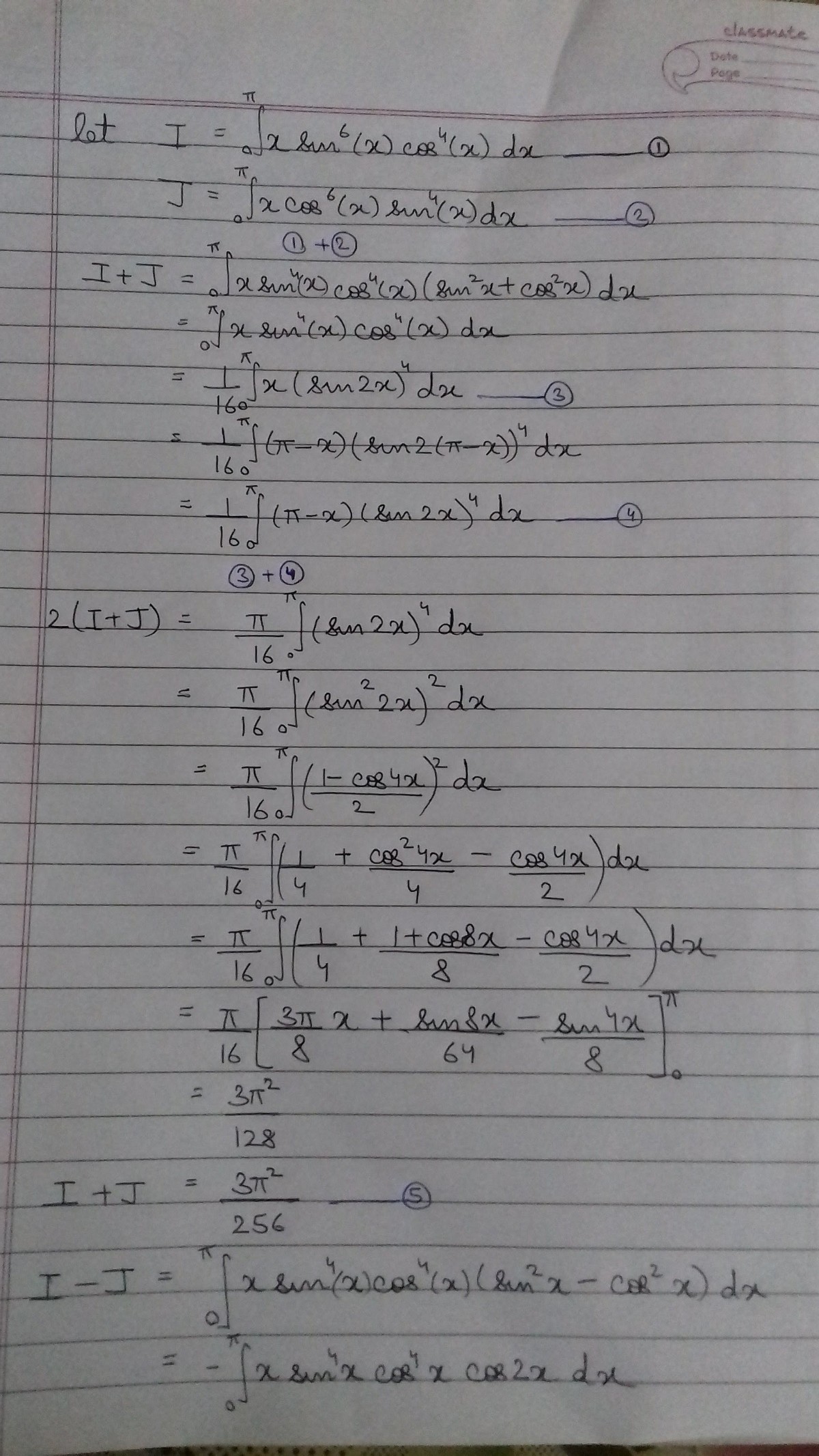
Using $f(a+b-x) \rightarrow f(x)$ the integral converts into

$\begin{aligned} I &= \int_{0}^{\pi}x \sin^{6} (x) \cos ^{4} (x) dx \\ &= \int_{0}^{\pi}(\pi - x) \sin^{6} (x) \cos ^{4} (x) dx \\ &= \pi \int_{0}^{\pi} \sin^{6} (x) \cos ^{4} (x) dx - \int_{0}^{\pi}x \sin^{6} (x) \cos ^{4} (x) dx \\ &= \pi \int_{0}^{\pi} \sin^{6} (x) \cos ^{4} (x) dx - I \end{aligned}$

$\begin{aligned} 2I &= \pi \int_{0}^{\pi} \sin^{6} (x) \cos ^{4} (x) dx \\ &= \pi \int_{0}^{\dfrac{\pi}{2}} \sin^{6} (x) \cos ^{4} (x) dx + \pi \int_{\dfrac{\pi}{2}}^{\pi} \sin^{6} (x) \cos ^{4} (x) dx \end{aligned}$

Taking the substitution $t= x-\dfrac{\pi}{2}$ in the latter integral in the previous step, we get that the first and last integral in the last step are equal.

$2I = 2 \pi \int_{0}^{\dfrac{\pi}{2}} \sin^{6} (x) \cos ^{4} (x) dx$ $I = \pi \int_{0}^{\dfrac{\pi}{2}} \sin^{6} (x) \cos ^{4} (x) dx$

Now, $\dfrac{1}{2} B(x,y) = \int_{0}^{\dfrac{\pi}{2}} \sin^{2x-1} (t) \cos ^{2y-1} (t) dt$ .

So, the above integral turns into

$\begin{aligned} I &= \pi \times \dfrac{1}{2}\times B \left(\dfrac{7}{2} , \dfrac{5}{2} \right) \\ &= \dfrac{\pi}{2} \times \dfrac{\Gamma \left(\dfrac{7}{2} \right) \Gamma \left(\dfrac{5}{2}\right)}{\Gamma (6)} \\ &= \dfrac{3 \pi ^2 }{512} \end{aligned}$