When will they collide?
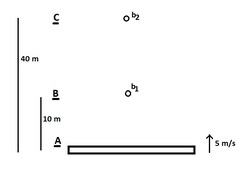 At
, 2 balls
and
are dropped from rest from heights of
and
respectively.
At
, 2 balls
and
are dropped from rest from heights of
and
respectively.
Also at , a very large heavy plank starts to move upward with speed .
Find the time (in sec) at which the balls collide for the first time.
Motion takes place in vertical plane
Assume all collisions as .
The plank still moves with speed after collision with the ball
The mass of the balls are negligible as compared to that of the plank.
The balls are to be considered point objects.
Collision takes negligible time
The answer is 2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Ball b 1 and the plank collide at t = 1 sec.
It is important to understand that the collision is elastic and the plank continues to move with v = 5 m / s after the collision.
The speed of the ball just before collision is u = g t , u = 1 0 m / s
The speed of the ball after collision v f 1 can be found out by equation of restitution. Since, collision is elastic, e = 1
v f 1 − 5 = 1 ( 5 − ( − 1 0 ) )
v f 1 = 2 0 m / s upwards.
Now the problem is converted into a simple kinematics problem.
At t = 1 sec, just after the collision b 1 is at a height of 5 m and b 2 is at a height of 4 0 − 2 1 g t 2 = 3 5 m .
Speeds of the balls are respectively, v f 1 = 2 0 m / s and v f 2 = 1 0 m / s
Using equations of kinematics, T can be easily found out.
3 0 = v f 1 ( T − 1 ) − 2 1 g ( T − 1 ) 2 + v f 2 ( T − 1 ) + 2 1 g ( T − 1 ) 2
Thus,
T = 2 sec.