When Wires Turn Useless
I guess I will never fall short of useless wire. This time I had a wire with a total resistance of 1 5 Ω and then I cut it into 30 equal pieces to form a regular Icosahedron as shown below. Then what is the equivalent resistance between any two opposite nodes in Ω ?
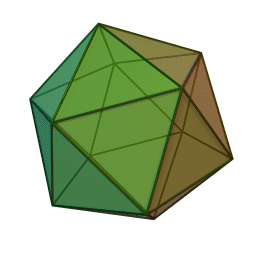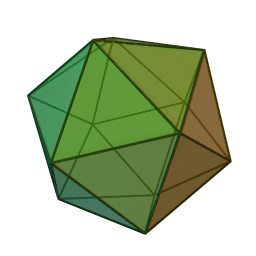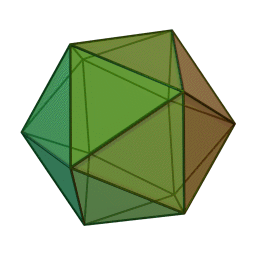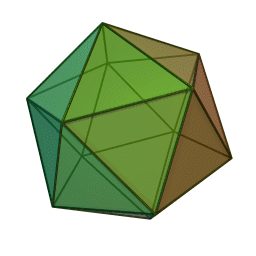
If the equivalent resistance between any two opposite nodes is R , then enter the value of 1 0 0 R .
Image credit:Wikipedia
This question is part of the set Platonic Electricity .
The answer is 25.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Oh my god (+1)
Best solution ever seen regarding Resistance! (+1)
Hm... I dont know why, but this formula works for most of such figures,
The resistance between two opposite nodes =
No. of edges
+
No. of parts
Total resistance
In this figure it is
3
0
+
3
0
1
5
=
6
0
1
5
=
0
.
2
5
So,
1
0
0
R
=
2
5
@Ashish Siva , does it work for every hedron? And what do you mean by parts?
Ha ha, even I am not able to understand how it's working. :D
The total wire was of 1 5 Ω , divided into 3 0 branches. That means each branch is of 0 . 5 Ω .
The figure above shows the sides of the regular Icosahedron, joined by the set of points ( A − L ) . A and L are opposite to each other and hence will be followed in the solution.
Now, points B , C , D , E , F are at same potential, because:
because of this , the resistances in between ( B a n d C ) , ( C a n d D ) , ( D a n d E ) , ( E a n d F ) , ( F a n d B ) becomes dead, and will not be counted in the final circuit.
Now, the current again divides equally at each of the points B , C , D , E , F into two parts. which means the current between the branches which can be seen in the circuit that are ( B , G ) , ( C , G ) , ( C , H ) , ( D , H ) , ( D , I ) , ( E , I ) and others which makes a total of 10 resistances in which the current flowing is 1 0 I .
Again the points G , H , I , J , K are at same potential and again the resistances joining these in between these nodes become dead. At last we are left with five resistances in between G , H , I , J , K , L and L , which will again be in parallel.
Now, we have 5 resistance in parallel which is in series with 1 0 resistance in parallel which again is in series with 5 resistance in parallel.
So, total resistance R = ( A , B ) , ( A , C ) , ( A , D ) , ( A , E ) , ( A , F ) 5 2 1 + 1 0 p a r a l l e l r e s i s t a n c e 1 0 2 1 + ( L , G ) , ( L , H ) , ( L , I ) , ( L , J ) , ( L , K ) 5 2 1 = 4 1 = 0 . 2 5
1 0 0 R = 2 5