Where are you, Nene?
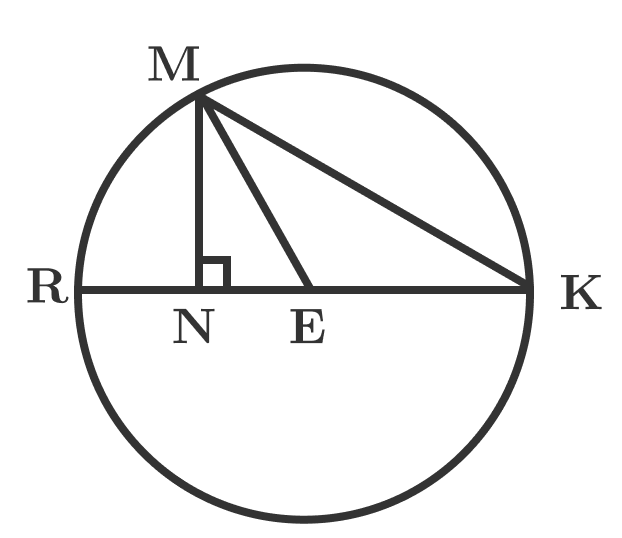
The circle above has center E , diameter R K = 2 4 m and ∠ R E M = 6 0 ∘ . Find the length of the line segment N E in meters.
The answer is 6.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
E M = 2 1 R K = 1 2
⇒ N E = 1 2 cos 6 0 ∘ = 6
ME = RE = RK/2 = 12
Triangle MER will have two sides equal and the third angle will be 60 degree. So rest two angles will also be 60 degrees hence it will be an equilateral triangle.
So perpendicular from its one vertex to opposite side will bisect.
Hence NE = 12/2 = 6
The triangle formed is a 30 60 90. Because RK is 24m, the radius, EM, is 12m. This means EN is half EM, therefore the answer is 6m.
Radius of a circle =12 cm.. Angle MNE 90 degree, Angle MEN = 60 Degree , Angle NME = 30 Degree. In triangle MNE Side NE is infront of 30 Degree, It is half of side ME. ie 6. ME is radius [Half of diameter.] Hence ME = 12 cm.
As the diameter is 2 4 m this gives r = 1 2 m and N E = r cos ( 6 0 ) N E = 6 m