Where do I look at this from? (1)
Consider a circle S 1 ,
x 2 + y 2 + 1 − 2 x ( cos θ − sin θ ) − 2 y ( cos θ + sin θ ) = 0
Now, consider another circle S 2 ,centred at P = ( − cos θ − sin θ , cos θ − sin θ ) such that S 1 internally touches S 2 .
Draw a pair of tangents T 1 and T 2 from P to S 1 .Let these tangents meet the circle S 2 at points A and B as shown. From a point R on S 2 , draw chords R A and R B with lengths l 1 , l 2 , respectively to S 2 .
Find the area of the shaded portion in the diagram below.
If you are looking for more such simple but twisted questions, twisted problems for jee aspirants is for you!
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
I did it by a bit lengthier method. I did it by calculating areas. First I found out the distance between centres of two circles. Then, I found the radius of given Circle, S1. Now that I got these two, I found the angle between tangents. So I calculated the area enclosed between the tangents and circle, S1. Now, I calculated the area of the bigger sector in which the smaller circle, S1 is present. I equated this area to sum of area between tangents and smaller circle, S1 + area of smaller circle S1+ two leftover areas(which are equal because of symmetry). I solved this equation and got the area. But still, this method is a bit lengthy. Rohith M.Athreya's solution is unique and simple.
I did the same way but made calculation mistake.
the title must have given u a hint that transformation of axes may help
let's set X = x c o s θ + y s i n θ − 1
Y = y c o s θ − x s i n θ − 1
this physically,is moving the origin of co-ordinate axes to ( 1 , 1 ) and then rotating the axes by an angle θ
S 1 in the new referrence frame is X 2 + Y 2 − 1 = 0 and the point P is ( − 2 , 0 )
from here it is plain geometry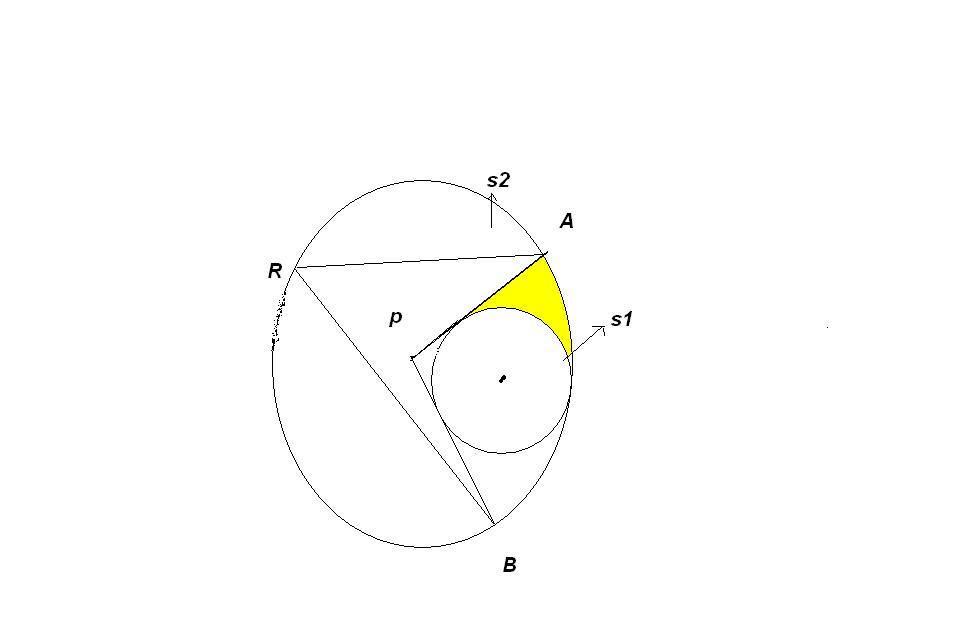
let O be centre of S 1 and E be the point of tangency of AP with S 1 and F be the point of tangency of BP with S 1
angle APB is π / 3
if D be the point of meeting of circles, angle APD is π / 6
we find area of sector APD and then subtract half of the area of S 1 = 2 π subtract the area of triangle O P E = 2 3 and add half the area of sector O E F = 6 π
this gives us 1 2 5 π − 2 3