Where Do They Intersect?

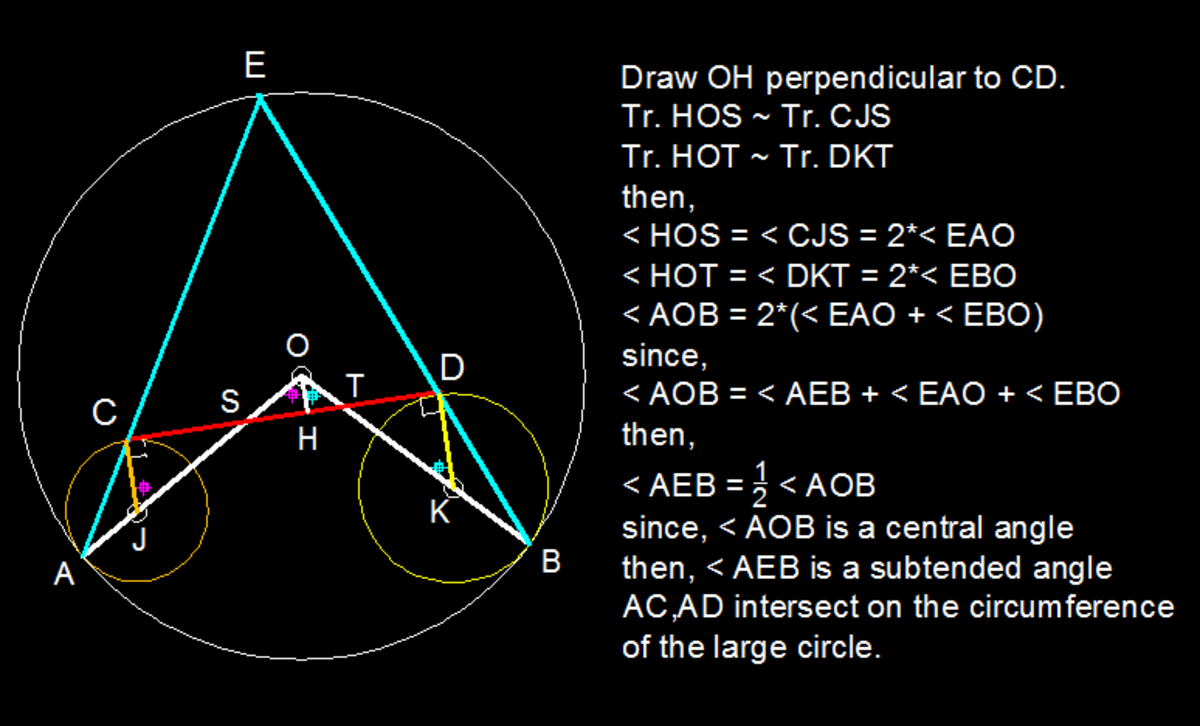
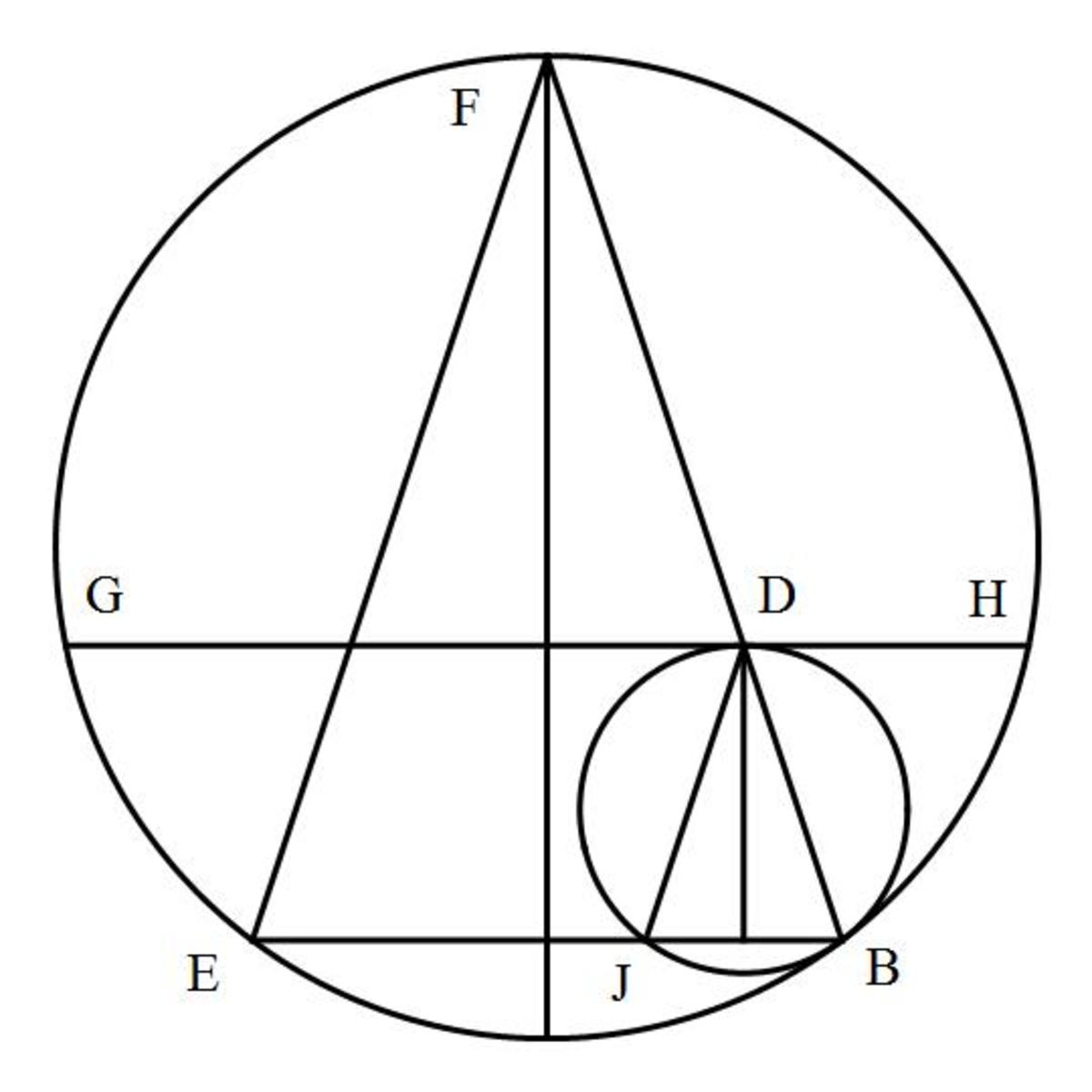
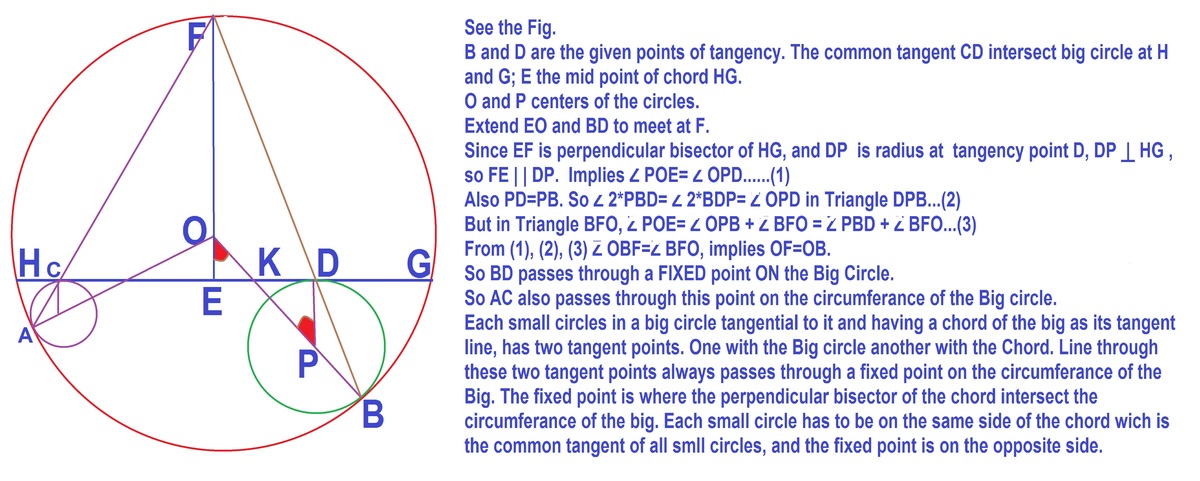
Claim: The line AC intersects the large circle at a point $P_{AC}$ , such that the tangent to the large circle is parallel to $CD$ .

Proof: Think about the expansion about point A, which brings the small circle to the large circle.
The image of point C will be moving along the line AC. The image of point C will also lie on the large circle. Hence, the image of point C will be $P_{AC}$ .
The tangent CD will continue to have the same slope, so the tangent at the image of point C will have the same slope as CD, thus they are parallel.

Claim: The line BD intersects the large circle at a point $P_{BD}$ , such that the tangent to the large circle is parallel to $CD$ .

Proof: Similar to previous claim

Claim: $P_{AC} = P_{BD}$

Proof: The tangents at these points have the same slope, and lie on the same side of $CD$ which intersects the circle. There is a unique point that satisfies these conditions.

Hence, the lines intersect on the circle, at a point which is tangential to CD.

---

The idea presented here is known as homothety , which is one of my favourite results in Euclidean Geometry. This problem is one of my favourite ones to demonstrate it's power in simplicity.

All roads lead to Rome, which is point F, on line perpendicular to arbitrary chord GH through its midpoint. Arbitrary small circle is tangent to chord GH at D and to large circle at B. Triangles BJD and BEF are similar isosceles triangles, and both vertical lines are their altitudes.

Given any arbitrary chord GH, line BD passes through point F on the large circle for any small circle tangent to GH at point D and to large circle at point B.

As shown By Calvin Lin, the fixed point is the point of tangentcy of the big circle parallel to the common tangent on the opposite side.

Two internally tangent circles

Extend AC to meet the outer circle at E. Draw radius OE. Point of tangency A and centers C1, O will be collinear. Do the same for the other circle with center C2

Triangles ACC1 and AEO are both isosceles, share an angle and the base. So they must be similar. And radius OE will be parallel to CC1 For the same reason, we must have a radius parallel to DC2. But since CC1 and DC2 are parallel (both perpendicular to the same tangent) So the two radii must merge giving a unique point E.