Where do you see lots of Asians?
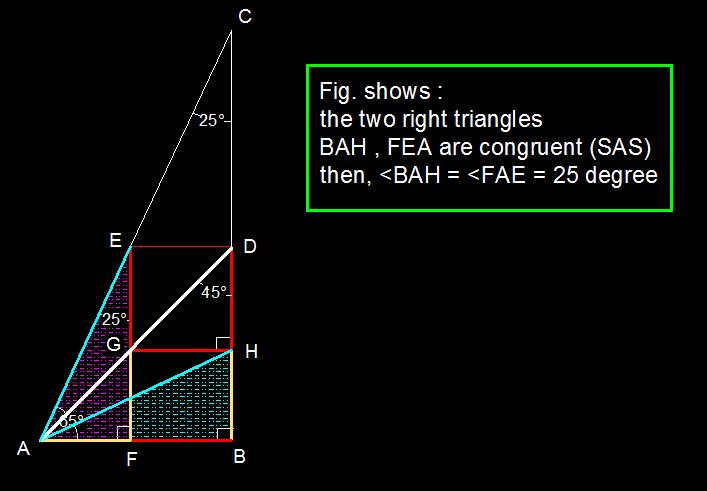
A B C satisfies ∠ B = 9 0 ∘ , ∠ A = 6 5 ∘ . Let D , E , F be on segments B C , A C , A B respectively such that E F = B D = A B and E F ∣ ∣ B C . Let A D ∩ E F = G and H is the foot of projection from G onto B C , Find ∠ B A H in degrees.
Answer to title: UCLA, because the university acronym could stand for U(you) C(see) L(lots) of A(asians), and the place is indeed known for having a large percentage of asian students.
The answer is 25.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Since B D = F E ∣ ∣ B C , D lies on B C , and F lies on A B , you can deduce that B D E F is a rectangle snugly against A B and B C .
F G E and B D C are both straight lines, and B F , D G and C E all meet at A . From this, we deduce that G splits F E in the same ratio as D splits B C . In other words, F G F E = B D B C . But F E = B D by construction, therefore B C . F G = ( F E ) 2 .
If we let A B = 1 , then F E = 1 by construction, and B C = tan 6 5 ∘ . Then we have F G = cot 6 5 ∘ = tan 2 5 ∘ . But B H G F is a rectangle, therefore F G = B H . So B H = tan 2 5 ∘ ⇒ B A B H = tan 2 5 ∘ ⇒ ∠ B A H = 2 5 ∘ .
(Coordinate Geometry FTW)
(Please draw a diagram to comprehend this)
Let B be origin, A be (0,1), C be ( tan 6 5 ∘ ,0).
Then, eqn. of AC: ( tan 6 5 ∘ ) y + x = tan 6 5 ∘ .
D is (1,0), BDEF is a rectangle, so x-coordinate of E is 1.
E lies on AC, so sub. x=1 to eqn. of AC to get y = tan 6 5 ∘ tan 6 5 ∘ − 1 .
That is the y-coordinate of E.
Eqn. of AD: x + y = 1 .
Eqn. of EF: y = tan 6 5 ∘ tan 6 5 ∘ − 1 .
Solve, x = tan 6 5 ∘ 1 = tan 2 5 ∘ .
Therefore, H is ( tan 2 5 ∘ ,0).
BAH is a right-angled triangle, and tan ∠ B A H = 1 tan 2 5 ∘ .
Therefore, ∠ B A H = 2 5 ∘ .