Where does the smallest square lie?
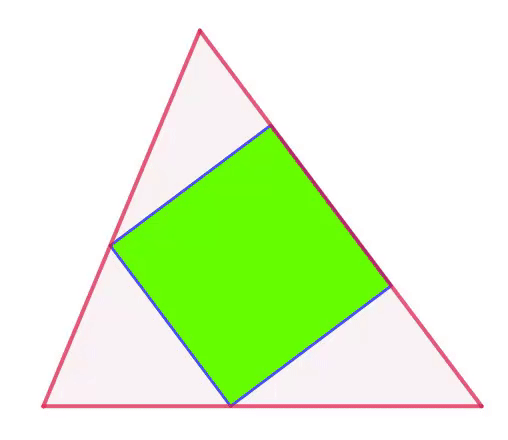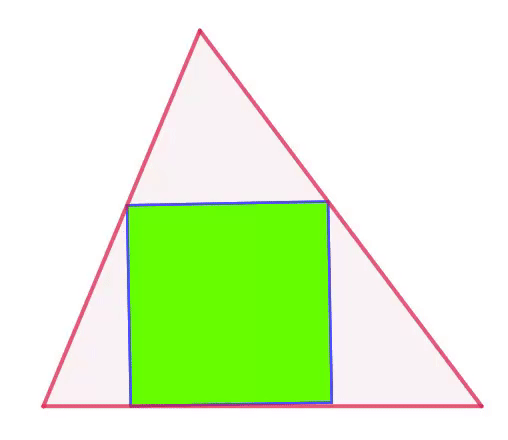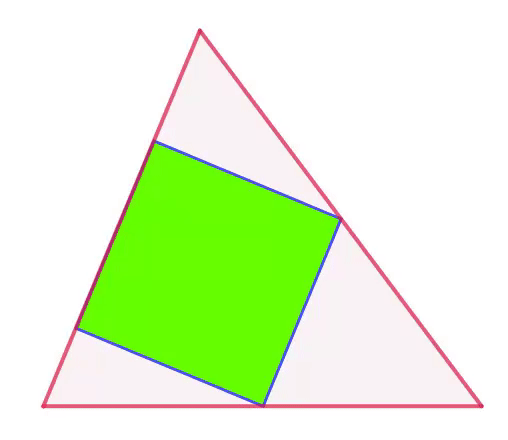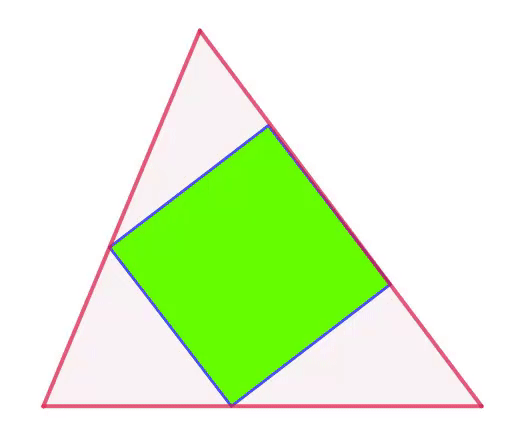 The triangle depicted in the animation has side lengths of
,
and
. The area of the smallest square which has at least three of its vertices on the sides of the triangle is
, where
and
are relatively prime positive integers. Find
.
The triangle depicted in the animation has side lengths of
,
and
. The area of the smallest square which has at least three of its vertices on the sides of the triangle is
, where
and
are relatively prime positive integers. Find
.
The answer is 28981.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Square K L M N has its vertices K , L and N on sides A B , A C and B C respectively as seen in figure 1. While K takes all possible positions on A B , angle θ c = ∠ A K L varies, with 9 0 ∘ − α ≤ θ c ≤ β . At the same time, the side length s c of the square changes. We want to determine the minimum value s c can take. Denote the length of segment B K by x .
Using Sine Rule on △ A K L ,
sin L A K = sin A K L ⇒ sin ( 1 8 0 ∘ − α − θ c ) c − x = sin a s c ⇒ sin ( α + θ c ) c − x = sin a s c ( 1 ) Using Sine Rule on △ B K N ,
sin N B K = sin B K N ⇒ sin ( 9 0 ∘ + θ − β ) x = sin β s c ⇒ x = sin β s c cos ( β − θ c ) ( 2 ) Combining ( 1 ) and ( 2 ) we get
s c [ sin ( α + θ c ) sin β + sin α cos ( β − θ c ) ] = c sin α sin β ( 3 ) Hence, s c is minimised when the function f ( θ c ) = sin ( α + θ c ) sin β + sin α cos ( β − θ c ) , 9 0 ∘ − α ≤ θ c ≤ β takes its maximum value.
Taking the derivative, f ′ ( θ c ) = cos ( α + θ c ) sin β + sin α sin ( β − θ c ) For the critical point,
f ′ ( θ c ) = 0 ⇔ cos ( α + θ c ) sin β + sin α sin ( β − θ c ) = 0 ⇔ ( cos α cos θ c − sin α sin θ c ) sin β + sin α ( sin β cos θ c − sin θ c cos β ) = 0 ⇔ sin θ c sin α ( sin β + cos β ) = cos θ c sin β ( sin α + cos α ) ⇔ cos θ c sin θ c = sin α ( sin β + cos β ) sin β ( sin α + cos α ) ⇔ tan θ c = sin α sin β sin α ( sin β + cos β ) sin α sin β sin β ( sin α + cos α ) ⇔ tan θ c = 1 + cot β 1 + cot α
Thus, the only zero of the function f ′ is at θ c ∗ = tan − 1 ( 1 + cot β 1 + cot α ) Furthermore, f ′ ′ ( θ c ) = − sin ( α + θ c ) sin β − sin α cos ( β − θ c ) < 0 for all θ c ∈ [ 9 0 ∘ − α , β ] . This means that the function f has a maximum at θ c ∗ . Consequently, from ( 3 ) we get the minimum for the side length of the square s c ∗ = sin ( α + θ c ∗ ) sin β + sin α cos ( β − θ c ∗ ) c sin α sin β ( 4 )
In order to calculate the exact value of s c ∗ we proceed to evaluate the trigonometric numbers of the angles of △ A B C .
Hence, sin β = 1 3 1 2 , cos β = 1 3 5 , cot β = 1 2 5 , sin γ = 1 5 1 2 = 5 4 , cos γ = 1 5 9 = 5 3 , cot γ = 1 2 9 = 4 3 .
Moreover, sin α = sin ( β + γ ) = sin β cos γ + sin γ cos γ = 6 5 5 6 , cos α = − cos ( β + γ ) = − cos β cos γ − sin β sin γ = 6 5 3 3 and cot α = cos α sin α = 5 6 3 3 .
Using these values we find tan θ c ∗ = 1 + cot β 1 + cot α = 1 + 1 2 5 1 + 5 6 3 3 = 2 3 8 2 6 7 Now, sin ( α + θ c ∗ ) = sin α cos θ c ∗ + sin θ c ∗ cos α = sin α ⋅ 1 + tan 2 θ c ∗ 1 + tan θ c ∗ ⋅ 1 + tan 2 θ c ∗ 1 ⋅ cos α = 6 5 5 6 ⋅ 1 + ( 2 3 8 2 6 7 ) 2 1 + 2 3 8 2 6 7 ⋅ 1 + ( 2 3 8 2 6 7 ) 2 1 ⋅ 6 5 3 3 = 5 7 5 7 1 3 1 And similarly, cos ( β − θ c ∗ ) = 7 5 7 2 6 .
Having all the ingredients,
( 4 ) ⇒ s c ∗ = 5 7 5 7 1 3 1 ⋅ 1 3 1 2 + 6 5 5 6 ⋅ 7 5 7 2 6 1 3 ⋅ 6 5 5 6 ⋅ 1 3 1 2 = 7 5 7 1 6 8 ≈ 6 . 1
Thus, the area of the smallest square with one vertex on side c and its opposite vertex moving inside the square is A = ( s c ∗ ) 2 = 7 5 7 2 8 2 2 4 ≈ 3 7 . 2 8 Working similarly, we find that the smallest square with one vertex on side a and its opposite vertex moving inside the square has area 3 6 5 1 4 1 1 2 ≈ 3 8 . 6 6 and the smallest square with one vertex on side b and the opposite one moving inside the square has area 7 0 1 2 8 2 2 4 ≈ 4 0 . 2 6 .
Comparing the results, we know that the area of the square in question is A = 7 5 7 2 8 2 2 4 .
For the answer, p + q = 2 8 2 2 4 + 7 5 7 = 2 8 9 8 1 .
Note :
f ′ ′ ( θ c ) < 0 , for all θ c ∈ [ 9 0 ∘ − α , β ] , hence f ′ is a decreasing function. Therefore, f ′ ( θ c ) > 0 for θ c ∈ [ 9 0 ∘ − α , θ c ∗ ) and f ′ ( θ c ) < 0 for θ c ∈ ( θ c ∗ , β ] . Consequently, f is increasing in [ 9 0 ∘ − α , θ c ∗ ] and decreasing in [ θ c ∗ , β ] ,giving its minimum when θ c = 9 0 ∘ − α , or θ c = β .
Eventually, when the largest square occurs, all its vertices lay on the sides of the triangle. This result holds, not only for the 1 3 - 1 4 - 1 5 triangle, but for all acute triangles.