Where is the oil?
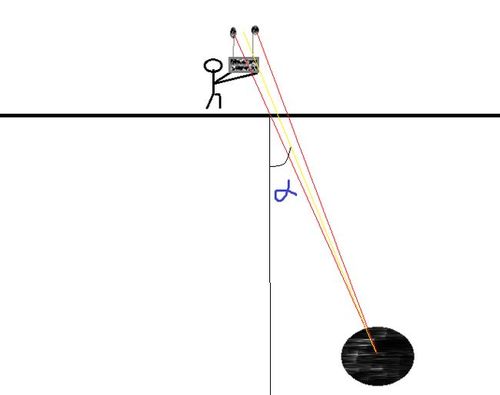 You have been hired by a tech-company you are designing a device witch can locate oil underground, the device consists a radio emission circuit and two signal receivers witch they are 20cm apart if the time delay of the signal between the receivers is 0.2ns what is
?.
You have been hired by a tech-company you are designing a device witch can locate oil underground, the device consists a radio emission circuit and two signal receivers witch they are 20cm apart if the time delay of the signal between the receivers is 0.2ns what is
?.
Details and assumptions
:
The speed of light is 300Mm per second.
The oil is far from the device.
Give your answer in degrees.
The answer is 17.457.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
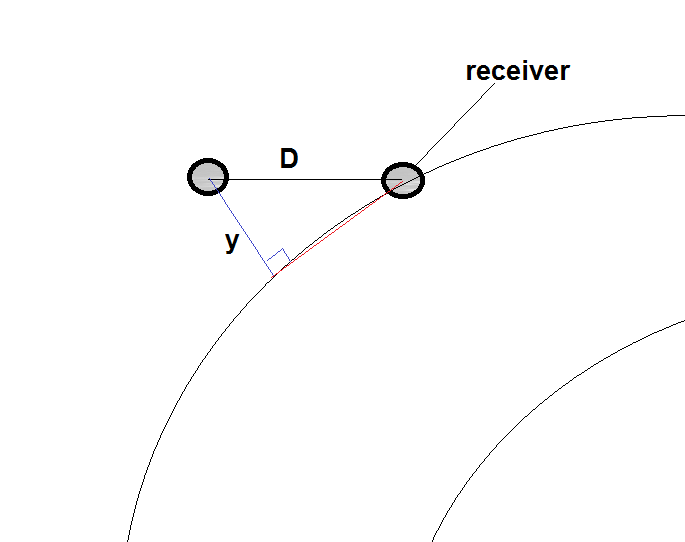
By writing cosine law for Δ A B C we get :
l 1 2 = l 2 2 + d 2 − 2 d l 2 cos ( 2 π − α )
Now, since l 1 , l 2 ≫ d we can write this equation as:
l 1 2 = l 2 2 − 2 d l 2 cos ( 2 π − α )
From this equation we can find sin α directly as:
sin α = 2 d l 2 l 2 2 − l 1 2 cos ( 2 π − α ) = cos 2 π cos α + sin 2 π sin α = sin α
By writing l 2 2 − l 1 2 as ( l 2 − l 1 ) ( l 1 + l 2 ) , we get:
sin α = 2 d l 2 ( l 2 − l 1 ) ( l 1 + l 2 ) = d ( l 1 − l 2 ) 2 l 2 ( l 1 + l 2 )
Again because l 1 , l 2 ≫ d we can say that l 2 l 1 ≈ 1 , because of this 2 l 2 ( l 1 + l 2 ) ≈ 1 .
And finaly l 2 − l 1 = c τ , by adding this we get:
sin α = d c τ ⇒ α = arcsin d c τ