Where is the triangle ?
Geometry
Level
2
If a triangle of area 9 square units is formed by the x-axis
and the lines x= 1 and y = mx - 4 (m < 0),
what are the coordinates of the vertices ?
(-8,0) (6,0) (1,8)
(-2,0) (1,0) (1,-6)
(-2,4) (1,5) (5,-6)
(2,3) (6,7) (9,8)
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
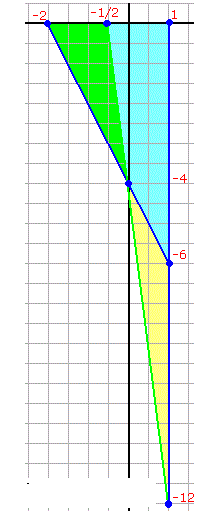
The x-axis is horizontal and the line x = 1 is vertical.
The third line with slope m < 0 goes from upper left to lower right, and intersects the y-axis at (0,-4). The line will intersect [x = 1] at (1,y) with y < -4, and the x-axis at (x,0) with x < 0.
Then the area of the triangle will be 1/2 (1-x) (-y) If that equals 9, then (1-x) (-y) = 18 or y (x-1) = 18.
Also, (y+4)/(1-0) = -4/(-x) = m ( slope from (x,0) to (0,-4) = slope from (0,-4) to (1,y) )
y+4 = 4/x (slope) xy + 4x = 4 xy - y = 18 (area) 4x + y = -14 (subtract) y = -4x - 14 Substituting back into the area equation, x(-4x-14) + 4x + 14 = 18 -4x^2 -14x + 4x - 4 = 0 -2x^2 - 5x -2 = 0 Roots are x = -2 and x = -1/2, with corresponding y values of -6 and -12.
So we have two possible triangles: (-2,0) (1,0) (1,-6) (area = 1/2 × 3 × 6) and (-1/2, 0) (1,0) (1,-12) (area = 1/2 × 1.5 × 12)