What´s The Radius?
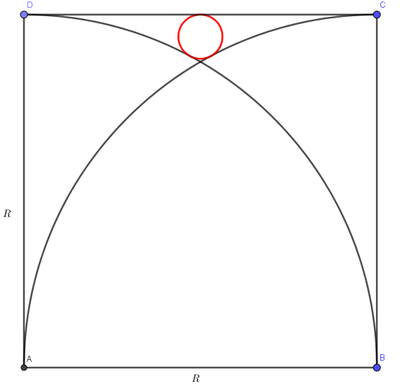
A B C D is a square with side length R . Find the radius of the red circle in terms of R .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
"and AO = R + r". I see this is the key insight. Took me a while to see where you were using the geometry of the curves. But I would take the problem writer to task for not explicitly saying that these are circular arcs. This proof wouldn't work for a pair of parabolic arcs.
Log in to reply
How would you solve it if they're parabolic arcs?
Log in to reply
Similar but more complicated calculations was we are dealing with two semi-axes instead of one radius.
I did it exactly the same way including using the same "r" for the radius.
Let the mid point of AB be E, r be the radius and F be the centre of the red circle. Then AF = R+r, AE = 2 R , and EF = R - r. Since the angle AEF is a right angle, therefore ( R + r ) 2 − ( R − r ) 2 = 4 R 2 . Or r= 1 6 R
If we draw a vertical line with the radius of the red circle until the side of the square, we can get a formula for this problem
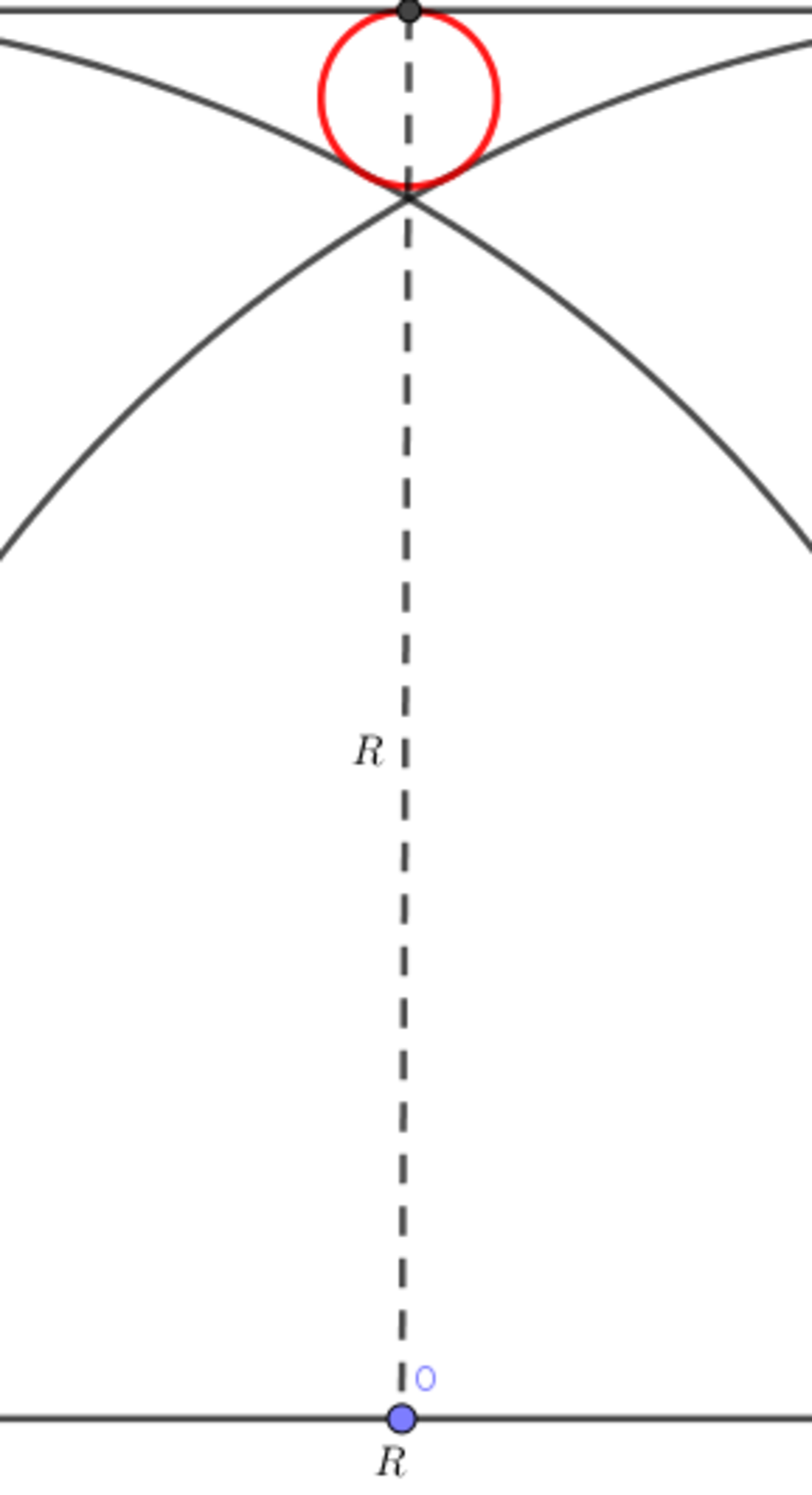 We can divide that line such that the sum of all these segments equals to
R
, like this:
We can divide that line such that the sum of all these segments equals to
R
, like this:
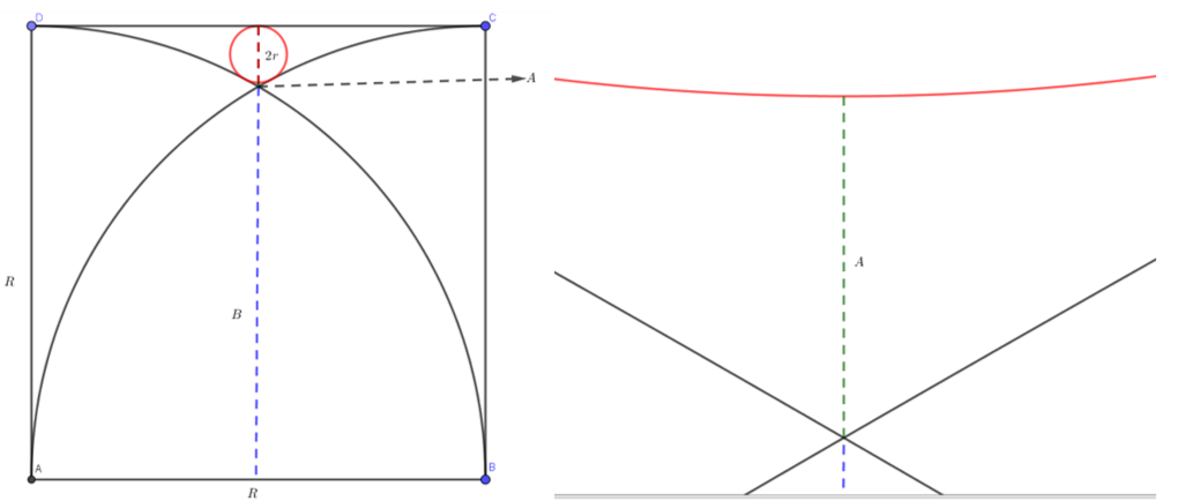 The radius of the circle
(
2
r
)
added with the lines a and b equal to
R
:
The radius of the circle
(
2
r
)
added with the lines a and b equal to
R
:
2 r + a + b = R . . . . . . . . . . . . . . . . . . ( 1 )
We can calculate b with the intersection point between B D ⌢ and C A ⌢ : Suppose that point A has coordinates ( 0 , 0 ) , now let´s find the equations of both circumferences.The center of B D ⌢ is ( 0 , 0 ) , so its equation is y = R 2 − x 2 and the center of C A ⌢ is ( R , 0 ) , so its equation is y = R 2 − ( x − R ) 2 . The intersection can be found with the equation
R 2 − x 2 = R 2 − ( x − R ) 2
Solving this, the intersection point is ( 2 R , 2 R 3 ) . In this case b is the y-coordinate of the intersection point.
Now, for
a
, we can draw a triangle with the center point of the red circle and points
A
,
B
.
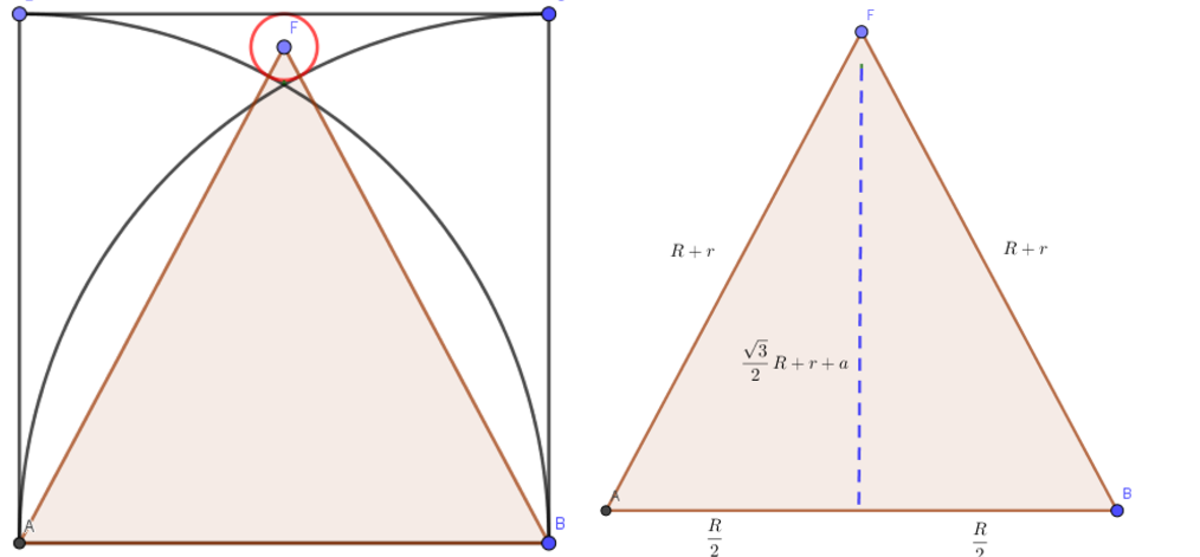 We can create a right triangle dividing the side of the square by 2, with lengths like the graph above. Use Pythagoras´ theorem to find
a
.
We can create a right triangle dividing the side of the square by 2, with lengths like the graph above. Use Pythagoras´ theorem to find
a
.
( 2 R ) 2 + ( r + 2 R 3 + a ) 2 = ( R + r ) 2
We can calculate r in terms of R and a using the first equation
R = 2 r + a + b = 2 r + a + 2 R 3 , with this, r = 4 R ( 2 − 3 ) − 2 a . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ( 2 )
Therefore, the new equation is
( 2 R ) 2 + ( 4 R ( 2 + 3 ) + 2 a ) 2 = ( 4 R ( 6 − 3 ) − 2 a ) 2
Solving this equation for a , a = 8 R ( 7 − 4 3 ) .
Finally, substitute a in the second equation
r = 4 R ( 2 − 3 ) − 2 ( 8 R ( 7 − 4 3 ) )
r = 1 6 R
Let the center and radius of the red circle be O and r respectively, M be the midpoint of C D and P be on D A such that O P is parallel to C D . Then we note that A P = R − r , O P = 2 R , and A O = R + r . By Pythagorean theorem , we have:
( R − r ) 2 + ( 2 R ) 2 4 R 2 ⟹ r = ( R + r ) 2 = ( R + r ) 2 − ( R − r ) 2 = 4 R r = 1 6 R