Where Will It Sag To?
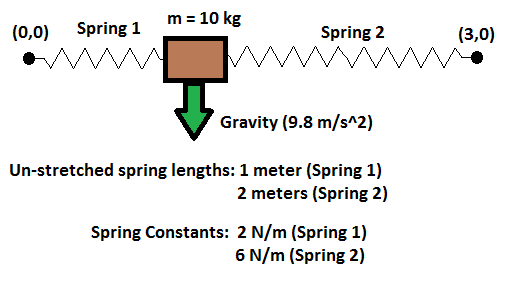
A mass (of negligible size) is attached to two initially un-stretched springs. The other end of each spring is anchored at a fix point, as shown in the picture. Spring parameters are shown in the picture. The mass falls from its initial position under the influence of gravity and of the springs.
Assuming that air resistance eventually brings the mass to rest, what is the sum of the absolute values of the equilibrium and coordinates?
All quantities are in SI units.
Feel free to solve using any method of your choosing.
The answer is 16.198.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
As far as I can tell, this one is actually rather tricky, because the equations depend non-linearly on the variables. I'm curious to see what people propose as solutions. I used a hill-climbing algorithm to solve it (or more properly, valley-descent). Essentially, randomly perturb the x and y coordinates of the mass slightly and see if the net force on the mass goes down relative to its previous position. Only accept alterations which lessen the net force. After a great many small perturbations, the program settles on a set of (x,y) coordinates that yields a net force of approximately zero.