Where'd The Extra Square Go?
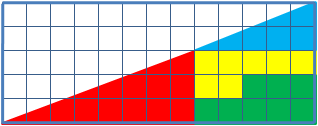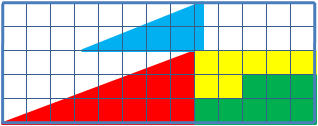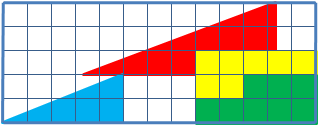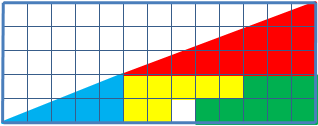
The shapes that make a triangle are rearranged to form a seemingly identical triangle, but with a square missing. How do you explain the missing square?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Nice use of pictures!
Wonderful solution, explained very neatly.
Wow, it is one of the few questions I really understand!!
Thanks for such a clear answer. I've already figured it out as soon as I saw the diagram of the problem, but this answer is really clear.
Clara B. provided a great solution, so I won't give one. But you might like to know that this puzzle is based on Fibonacci numbers...
The grid is 5x13, the blue and red triangle are 5x2 and 8x3, respectively, and the yellow/green rectangle changes from 5x3 to 8x2. All these are Fibonacci numbers: 1 , 1 , 2 , 3 , 5 , 8 , 1 3 , . . . where every number is equal to the sum of the previous ones: F n + 2 = F n + F n + 1 .
The slopes of the triangles are 2 5 (blue) and 3 8 (red); these fractions are close in value, which explains the puzzle. Note that both slopes are the ratio of Fibonacci numbers two apart. If we continue this pattern through the Fibonacci sequence, the ratios become more and more similar and converge to a special value: 2 5 , 3 8 , 5 1 3 , 8 2 1 , ⋯ , F n F n + 2 , ⋯ ⟶ ϕ 2 ≈ 2 . 6 2 . Here, ϕ ≈ 1 . 6 2 is the famous golden ratio , with the property ϕ 2 − 1 = ϕ .
For more fun, analyze the apparent change in area of the rectangle: it increased from 5 × 3 = 1 5 to 8 × 2 = 1 6 . If we use higher Fibonacci numbers, we get the same pattern:
-
8 × 5 = 4 0 but 1 3 × 3 = 3 9 ;
-
1 3 × 8 = 1 0 4 but 2 1 × 5 = 1 0 5 ;
-
2 1 × 1 3 = 2 7 3 but 3 4 × 8 = 2 7 2 ; etc.
Alternating, we seem to gain a unit of area and to lose a unit of area. This pattern continues throughout the Fibonacci sequence: F n + 2 F n + 1 = F n + 3 F n ± 1 . You want proof? I challenge you! Try to prove by induction.
Bonus: It is also true that F n + 1 2 = F n F n + 2 ± 1 , and there exists a similar puzzle based on this property. For instance, a square of dimensions 8x8 is cut into four parts, which are rearranged to form a rectangle of dimensions 5x13...
Woah! This is amazing! You should make a whole wiki page out of this, it deserves it
Such knowledge deserve to be shared Thanks that awesome
Amazing to know! Thanks!
The two small triangles have hypotenuses that are different slopes, just close enough to look identical: 2/5 = .4 and 3/8 = .375 (so close, but not equal!) When they move, the total area of all of the 4 shapes remains the same, but when there's a hole, it's because the combined-bent-hypotenuse of the big triangle has a bump outward. When there's no hole, it's because the combined-bent-hypotenuse has a dent inward.
And the area beneath the triangles is different between the two positions because, in the first case, the rectangular area beneath the two triangles is 8x2=16 squares, in the second case, it's 5x3 = 15 squares.
If the two small triangles were similar (had the same slope to their hypotenuse), such a disparity would be impossible. If the triangles were similar, than the ratios of the two legs of the larger "A/B" would be equal to the ratio of the legs of the smaller "C/D." The rectangular space beneath both triangles goes from an A-by-D rectangle to a B-by-C rectangle. If A/B = C/D, then AD = BC.