Where's The Centre?
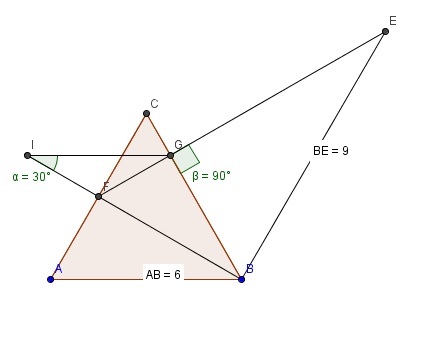
A B C is an equilateral triangle with side length 6
Point E is on the external angle bisector from B such that B E = 9 .
The perpendicular dropped from E to B C intersects B C at G and A C at F .
Point I is on line B F extended through F such that ∠ F I G = 3 0 ∘ .
The circumcenter of △ B I G is O
Find 8 × A O .
The answer is 12.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Draw a line passes point I and perpendicular to I G , it cuts the line that passes point B perpendicular to B G at D . Then B G I D is concylic, and the center O of the circumcircle is the midpoint of G D . Looks like O lies on A B , we're going to prove it.
∠ O B D = ∠ G D B = ∠ G I B = 3 0 ∘ ; therefore, ∠ G B A = 6 0 ∘ , which means A O B is a straight line (prove complete!)
∠ G D B = ∠ G E B = 3 0 ∘ ; also, E G is parallel to B D , so we have E G D B is a parallelogram. Then, D G = B E = 9 or O B = 4 . 5 . 'Cause A O B is a straight line, A O = A B − O B = 6 − 4 . 5 = 1 . 5 , which gives the answer 1 2 .
Bonus: In the diagram, looks like circle ( O ) and circle ( A , A B ) are tangent at B . Can you prove it?
Two circles are said to touch each other internally if the distance between their centres is equal to the absolute difference of the lengths of the two radii.In this case it is quite obvious as the difference between the two radii (that is AB-OB) is equal to the distance between the two centres (that is OA).So,the result follows.
Great image. That really helps your solution :)
∠ B I G = 3 0 ∘ ⇒ ∠ B O G = 6 0 ∘ (angle at centre is twice angle at radius)
O G = O B ⇒ ∠ O G B = ∠ O B G = 6 0 ∘ so △ O B G is equilateral.
∠ G B O = 6 0 ∘ ⇒ O is on line A B because ∠ C B A = 6 0 ∘
∠ E B G = 6 0 ∘ ⇒ G B = 9 cos ( 6 0 ∘ ) = 2 9 (external bisector+sine rule)
B O = G B = 2 9 as △ B O G is equilateral.
A O = A B − B O = 6 − 2 9 = 2 3 because A O B is a straight line.
8 × A O = 8 × 2 3 = 1 2
Moderator note:
Great observation that O lies on AB, which makes the rest of the problem easier to track.
Did it the same way.
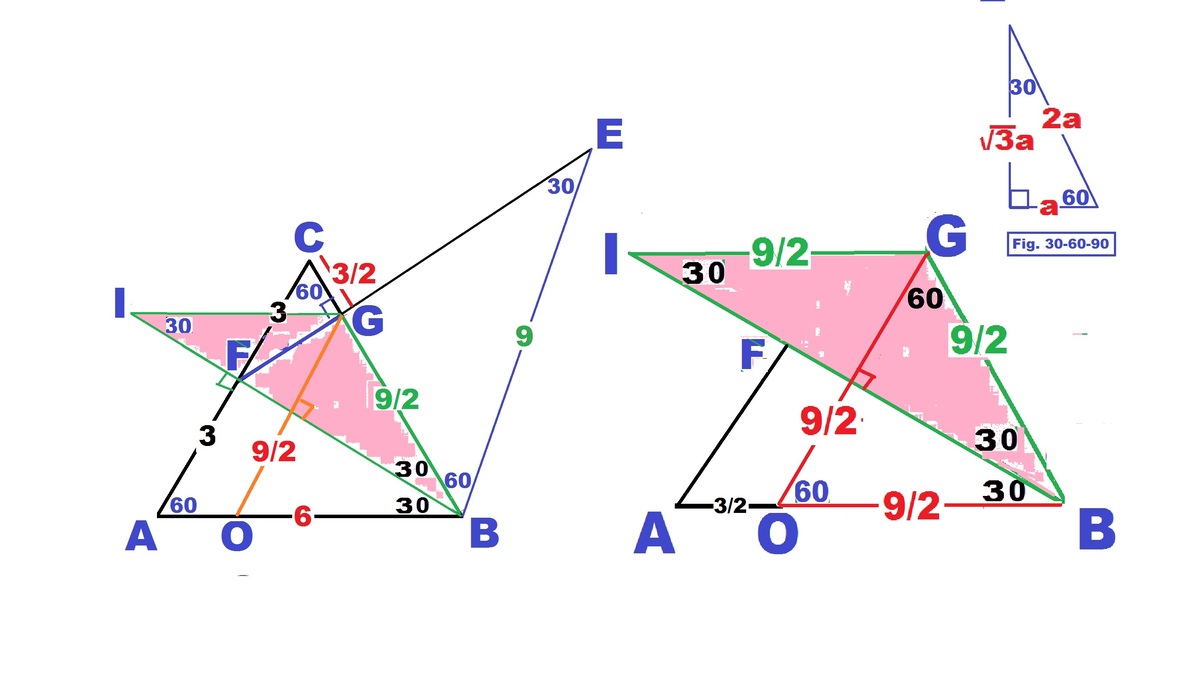 F
i
g
.
3
0
−
6
0
−
9
0
s
h
o
w
s
t
h
e
r
e
l
a
t
i
o
n
s
i
n
a
3
0
−
6
0
−
9
0
Δ
,
u
s
e
d
b
e
l
o
w
.
∠
G
B
E
=
2
1
∗
(
1
8
0
−
6
0
)
=
6
0
.
Δ
i
s
3
0
−
6
0
−
9
0
.
∴
G
B
=
9
/
2
a
n
d
C
G
=
3
/
2
,
a
n
d
∠
C
F
G
=
3
0
.
B
u
t
G
C
F
i
s
a
l
s
o
3
0
−
6
0
−
9
0
.
∴
C
F
=
3
,
⟹
F
i
s
t
h
e
m
i
d
p
o
i
n
t
o
f
A
C
.
∴
B
F
i
s
⊥
b
i
s
e
c
t
o
r
a
s
w
e
l
l
a
s
a
n
g
l
e
b
i
s
e
c
t
o
r
o
f
A
C
.
⟹
∠
I
F
G
=
∠
I
F
C
+
∠
C
F
G
=
1
2
0
a
n
d
∠
I
B
G
=
3
0
.
⟹
Δ
B
I
G
i
s
i
s
o
s
c
e
l
e
s
.
I
t
s
c
i
r
c
u
m
r
a
d
i
u
s
R
=
4
∗
a
r
e
a
.
p
r
o
d
u
c
t
o
f
s
i
d
e
s
.
R
=
4
∗
2
1
∗
(
2
9
∗
3
)
∗
(
2
1
∗
2
9
)
(
2
9
)
2
∗
(
2
9
∗
3
)
=
9
/
2
=
G
O
.
G
O
=
G
B
,
∠
G
B
A
=
6
0
,
⟹
Δ
G
O
B
i
s
e
q
u
i
l
a
t
e
r
a
l
∴
O
B
=
9
/
2
.
⟹
A
O
=
3
/
2
.
∴
8
∗
A
O
=
1
2
F
i
g
.
3
0
−
6
0
−
9
0
s
h
o
w
s
t
h
e
r
e
l
a
t
i
o
n
s
i
n
a
3
0
−
6
0
−
9
0
Δ
,
u
s
e
d
b
e
l
o
w
.
∠
G
B
E
=
2
1
∗
(
1
8
0
−
6
0
)
=
6
0
.
Δ
i
s
3
0
−
6
0
−
9
0
.
∴
G
B
=
9
/
2
a
n
d
C
G
=
3
/
2
,
a
n
d
∠
C
F
G
=
3
0
.
B
u
t
G
C
F
i
s
a
l
s
o
3
0
−
6
0
−
9
0
.
∴
C
F
=
3
,
⟹
F
i
s
t
h
e
m
i
d
p
o
i
n
t
o
f
A
C
.
∴
B
F
i
s
⊥
b
i
s
e
c
t
o
r
a
s
w
e
l
l
a
s
a
n
g
l
e
b
i
s
e
c
t
o
r
o
f
A
C
.
⟹
∠
I
F
G
=
∠
I
F
C
+
∠
C
F
G
=
1
2
0
a
n
d
∠
I
B
G
=
3
0
.
⟹
Δ
B
I
G
i
s
i
s
o
s
c
e
l
e
s
.
I
t
s
c
i
r
c
u
m
r
a
d
i
u
s
R
=
4
∗
a
r
e
a
.
p
r
o
d
u
c
t
o
f
s
i
d
e
s
.
R
=
4
∗
2
1
∗
(
2
9
∗
3
)
∗
(
2
1
∗
2
9
)
(
2
9
)
2
∗
(
2
9
∗
3
)
=
9
/
2
=
G
O
.
G
O
=
G
B
,
∠
G
B
A
=
6
0
,
⟹
Δ
G
O
B
i
s
e
q
u
i
l
a
t
e
r
a
l
∴
O
B
=
9
/
2
.
⟹
A
O
=
3
/
2
.
∴
8
∗
A
O
=
1
2
Here is a solution using complex numbers.Let point A be the origin in the argand plane.We denote cos(x)+isin (x)=cis (x).In triangle ABC ,rotation about A gives c=bcis (pi/3) where b and c are complex numbers corresponding to points B and C in the complex plane.Note that we take the angle of rotation to be positive in case of counter clockwise rotation.Suppose circumcenter of triangle BIG is denoted by z.We have angle BOG=2 times angle BIG=60 degrees.In triangle BOG,rotation about O gives (g-z)=(b-z)cis (pi/3).Rearranging and using c=bcis (pi/3),we get (g-c)=z (1-cis (pi/3)).Taking modulus on both sides,we get |g-c|=|z||(1-cis (pi/3)|.But |1-cis (pi/3)|=1.Hence,we get |z|=|g-c|=length of line segment CG.But |z|=length of line segment AO as A is the origin.Therefore,we conclude that lengths of line segments AO and CG are congruent.Now ,triangle BGC is a 30-60-90 triangle,hence we get BG=half of BE=4.5.Hence CG=BC-BG=6-4.5=1.5.Therefore AO=1.5.Hence we have the answer as 8 times 1.5=12.