Where's the Letter C?

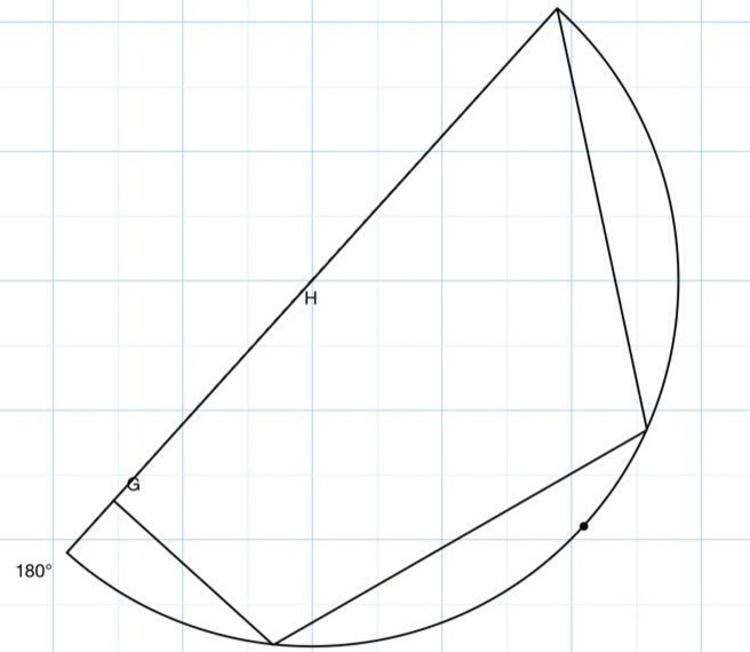We have a quadrilateral $DEFG$ inscribed in a semicircle with center $H$ such that point $G$ is on the diameter $AB$ of the semicircle and at the same time line $FG$ is perpendicular to $AB$ . Suppose that $2FG=DE=EF$ . Find the measure of $\angle GDE$ in degrees.

• Image Credit: Sir Trevor Arashiro

• The picture is only there to aid you, not all the letters are placed there

• Point $D$ coincides with either Point $A$ or $B$