Which center of triangle?
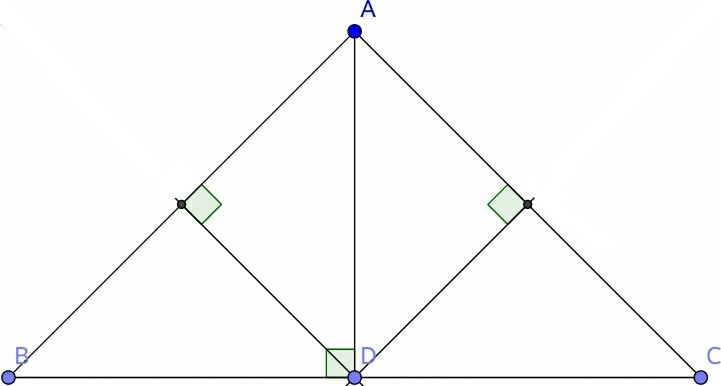 In the triangle above, what is point
with respect to the right isosceles
with
as the hypotenuse?
In the triangle above, what is point
with respect to the right isosceles
with
as the hypotenuse?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The point of intersection of all perpendicular bisectors of a triangle is the circumcenter of the triangle.
It is not the incenter because it is the point of intersection of the angular bisectors. While ∠ A B C and ∠ A C B is greater than 0 , ∠ B D B = ∠ C D C = 0 so, they are not the angular bisectors.
It is not the orthocenter because it is the point of intersection of altitudes, and ∠ B C A and ∠ A B C is not equal to 9 0 ° , so it is not an altitude.
It is not a centroid because it is the point of interesction medians and C and B are not the midpoints of A C and A B respectively. So, the answer is circumcenter.
Note :- In an isosceles triangle, the altitude is also its median, since AD is the altitude, it is also the median and thus the perpendicular bisector.