Which Formula Should I Apply? (Part 2)
Evaluate
2 − cot 2 ( 9 ∘ ) 2 4 1 + 2 − cot 2 ( 2 7 ∘ ) 2 4 1 + 2 − cot 2 ( 4 5 ∘ ) 2 4 1 + 2 − cot 2 ( 6 3 ∘ ) 2 4 1 + 2 − cot 2 ( 8 1 ∘ ) 2 4 1 .
The answer is 365.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
@Chew-Seong Cheong , we really liked your comment, and have converted it into a solution. If you subscribe to this solution, you will receive notifications about future comments.
can you explain how you went from the 7th line to the 8th line. i thought you used the double angle formula on 6(sin9cos9)^2 - 1 in the 7th line but if that's the case, i don't see how the constant term can change to -4 in the following line. did you apply some other trick? thanks!!!
Log in to reply
There is no trick. Write the calculation out.
Hint: sin θ cos θ = 2 1 sin 2 θ .
Log in to reply
OH...i get it now, sorry i simplified the numerator and found that it didn't match the next line when i should have simplified numerator and denominator and change the fractional coefficients into integers. that way, i'll get the same form as in line 8. thanks for the help!!!!!!!
can be solved in a much easier way if you use eulers identity, this corresponds to cos(10x)=0 which gives the roots as (2 n-1) pi/20 where n varies from 1 to 10
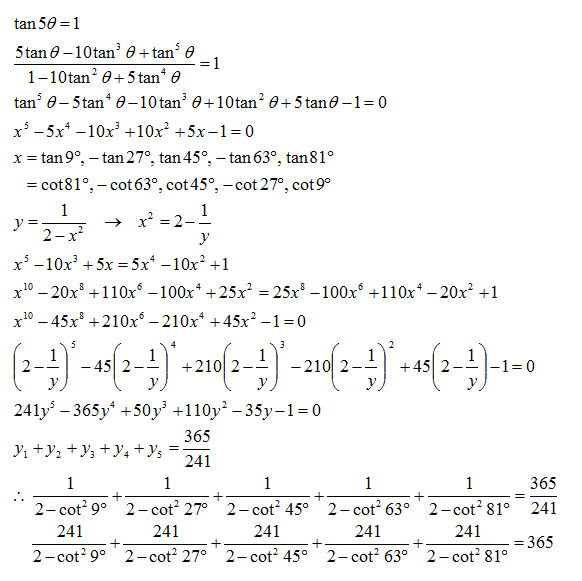
2 − cot 2 9 ∘ 2 4 1 + 2 − cot 2 2 7 ∘ 2 4 1 + 2 − cot 2 4 5 ∘ 2 4 1 + 2 − cot 2 6 3 ∘ 2 4 1 + 2 − cot 2 8 1 ∘ 2 4 1 = 2 − cot 2 9 ∘ 2 4 1 + 2 − cot 2 8 1 ∘ 2 4 1 + 2 − cot 2 2 7 ∘ 2 4 1 + 2 − cot 2 6 3 ∘ 2 4 1 + 2 4 1 = 2 4 1 ( 2 sin 2 9 ∘ − cos 2 9 ∘ sin 2 9 ∘ + 2 sin 2 8 1 ∘ − cos 2 8 1 ∘ sin 2 8 1 ∘ + 2 sin 2 2 7 ∘ − cos 2 2 7 ∘ sin 2 2 7 ∘ + 2 sin 2 6 3 ∘ − cos 2 6 3 ∘ sin 2 6 3 ∘ + 1 ) = 2 4 1 ( 3 sin 2 9 ∘ − 1 sin 2 9 ∘ + 3 sin 2 8 1 ∘ − 1 sin 2 8 1 ∘ + 3 sin 2 2 7 ∘ − 1 sin 2 2 7 ∘ + 3 sin 2 6 3 ∘ − 1 sin 2 6 3 ∘ + 1 ) = 2 4 1 ( 3 sin 2 9 ∘ − 1 sin 2 9 ∘ + 3 cos 2 9 ∘ − 1 cos 2 9 ∘ + 3 sin 2 2 7 ∘ − 1 sin 2 2 7 ∘ + 3 cos 2 2 7 ∘ − 1 cos 2 2 7 ∘ + 1 ) = 2 4 1 ( 9 sin 2 9 ∘ cos 2 9 ∘ − 3 sin 2 9 ∘ − 3 cos 2 9 ∘ + 1 3 sin 2 9 ∘ cos 2 9 ∘ − sin 2 9 ∘ + 3 sin 2 9 ∘ cos 2 9 ∘ − cos 2 9 ∘ + . . . + 1 ) = 2 4 1 ( 9 sin 2 9 ∘ cos 2 9 ∘ − 2 6 sin 2 9 ∘ cos 2 9 ∘ − 1 + 9 sin 2 2 7 ∘ cos 2 2 7 ∘ − 2 6 sin 2 2 7 ∘ cos 2 2 7 ∘ − 1 + 1 ) = 2 4 1 ( 9 sin 2 1 8 ∘ − 8 6 sin 2 1 8 ∘ − 4 + 9 sin 2 5 4 ∘ − 8 6 sin 2 5 4 ∘ − 4 + 1 ) = 2 4 1 ( 9 ( 2 1 − cos 3 6 ∘ ) − 8 6 ( 2 1 − cos 3 6 ∘ ) − 4 + 9 ( 2 1 − cos 1 0 8 ∘ ) − 8 6 ( 2 1 − cos 1 0 8 ∘ ) − 4 + 1 ) = 2 4 1 ( 9 cos 3 6 ∘ + 7 6 cos 3 6 ∘ + 2 + 9 cos 1 0 8 ∘ + 7 6 cos 1 0 8 ∘ + 2 + 1 ) = 2 4 1 ( 8 1 cos 3 6 ∘ cos 1 0 8 ∘ + 6 3 ( cos 3 6 ∘ + cos 1 0 8 ∘ ) + 4 9 1 0 8 cos 3 6 ∘ cos 1 0 8 ∘ + 6 0 ( cos 3 6 ∘ + cos 1 0 8 ∘ ) + 2 8 + 1 ) See Note = 2 4 1 ( 8 1 ( − 4 1 ) + 6 3 ( 2 1 ) + 4 9 1 0 8 ( − 4 1 ) + 6 0 ( 2 1 ) + 2 8 + 1 ) = 2 4 1 ( 6 0 . 2 5 3 1 + 1 ) = 3 6 5
Note:
We note that z 5 = e 5 2 k π = e 3 6 k ∘ = 1 are the 5 t h roots of unity. From Argand's diagram, we have:
{ cos 3 6 ∘ + cos 1 0 8 ∘ = 2 1 cos 7 2 ∘ + cos 1 4 4 ∘ = − 2 1 . . . ( 1 ) . . . ( 2 )
( 2 ) : cos 7 2 ∘ + 2 cos 2 7 2 ∘ − 1 4 cos 2 7 2 ∘ + 2 cos 7 2 ∘ − 1 = − 2 1 = 0
⇒ cos 7 2 ∘ ⇒ 2 cos 2 3 6 ∘ − 1 cos 2 3 6 ∘ ⇒ cos 3 6 ∘ = 4 5 − 1 = 4 5 − 1 = 8 5 + 3 = 1 6 2 5 + 6 = 1 6 ( 5 + 1 ) 2 = 4 5 + 1
( 1 ) : cos 1 0 8 ∘ = 2 1 − cos 3 6 ∘ = 2 1 − 4 5 + 1 = 4 1 − 5
⇒ cos 3 6 ∘ cos 1 0 8 ∘ = 4 1 − 5 × 4 5 + 1 = − 4 1