Which giant number is greater?
Which is greater,
3 5 3 or 6 2 6 ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
8 solutions
I would not expect a correct answer to have the word "clearly" in it. How can I know that 3 6 1 > 2 6 4 without calculations?
Log in to reply
3 6 1 > 8 ∗ 2 6 1 3 > 2 6 1 8 1 . 5 > 6 1 8 this is true since 1 . 5 > 6 8 which doesn't need calculations.
Log in to reply
Fair enough, but you've done some calculations to prove something that 'doesn't need calculations'. :-)
Nice solution and question.
I completely misread this. I thought it was [ 3 5 ] 3 . Oops...
I was trying another way which looked good at first, but I don't know how to go on
6 = 3 lo g 3 6
So we have
3 1 2 5 and 3 lo g 3 ( 6 ) 6 4
which brings us to
1 2 5 > lo g 3 ( 6 ) 6 4
Which is true if
lo g 3 6 < 6 4 1 2 5
6 < 3 6 4 1 2 5
but 3 6 4 1 2 5 > 3 1 + 2 1 + 4 1 = 3 ∗ 3 1 / 2 ∗ 3 1 / 4
is there a "polite" way to estimate those numbers without brutal calculation?
Log in to reply
raise both side ^4 3 1 6 1 2 5 > 3 ∗ 3 2 ∗ 3 4 = 3 ∗ 9 ∗ 8 1 = 2 1 8 7 > 6 4 = 1 2 9 6
why exactly 3^{125} and 6^{64} ?
6 2 6 = 2 2 6 × 3 2 6 < 3 2 6 + 1 = 3 4 3 + 1 3 < 3 5 3
I interpreted the expressions in the problem statement like so: [(a^b)^c] becomes [a^(b*c)]. Now I know what the colors of "b" and "c" terms mean.
2^64=2^9.2^55=512.2^55<729.3^55=3^61
Here's how I see the problem. When you have an exponent to another exponent, which is the case with this problem you use the Power Rule for Exponents. The power rule says to multiply the exponents and keep the base:
( x m ) n = x m n = x m ⋅ n . This same applies for this problem. Using the power rule,
3 5 3 = ( 3 5 ) 3 = 3 1 5 and 6 2 6 = ( 6 2 ) 6 = 6 1 2 . You can rewrite 6 1 2 as ( 2 ⋅ 3 ) 1 2 = 2 1 2 ⋅ 3 1 2 using the "product to a power rule". Now we can compare the two number by rewriting:
3 1 5 = 3 3 ⋅ 3 1 2 _ _ _ _ 2 1 2 ⋅ 3 1 2 = 6 1 2 . I obtained the left hand side by using the product rule for exponents in reverse. Now I can divide both sides of this inequality by 3 1 2 , assuming that both sides are not same, but even if they are I can still do this. Now I can compare 3 3 = 2 7 and 2 1 2 = 4 0 9 6 . Clearly 2 7 < 4 0 9 6 , therefore the other number, 6 2 6 is larger.
Log in to reply
( a b ) c = a ( b ∗ c ) a b c = a ( b c ) mind the brackets
Log in to reply
I see. In this case you work from the top down, not the bottom up. But I don't think I've every seen this rule before.
This exactly my explanation also. I also have been knowing this rule for so long.
Beautiful solution!
Awesome solution!
artistic manipulation! Worth praise!
That is beautiful.
Consider 6 2 6 3 5 2 = 2 6 4 3 6 4 3 1 2 5 = 2 6 4 3 6 1 = 2 6 4 ( 2 + 1 ) 6 1 = 2 6 4 2 6 1 + ( 6 1 ) 2 6 0 + ( 1 8 3 0 ) 2 5 9 + . . . = 2 6 4 ( 1 + 3 0 . 5 + 4 5 7 . 5 ) 2 6 1 + . . . = 2 6 4 ( 4 8 8 ) 2 6 1 + . . . = 2 6 4 ( 6 1 ) 2 6 4 + . . . > 1
⇒ 3 5 2 > 6 2 6
6 2 6 = 2 2 6 × 3 2 6 < 3 2 6 + 1 = 3 4 3 + 1 3 < 3 5 3
Option A: 3^(5^3) = 3^125 = 3^64 x 3^61 = 3^64 x 3^6 x 3^55 = 3^64 x 729 x 3^55
Option B: 6^(2^6) = 6^64 = 3^64 x 2^64 = 3^64 x 2^9 x 2^55 = 3^64 x 512 x 2^55
Since 729>512 and 3^55>2^55, Option A must be larger.
I divide each number in 6^2^6 →3^1^3 Compare with 3^5^3 and 3^1^3 so the bigger is 3^5^3
Consider ( 3 3 3 3....( 125 terms)) / ( 6 6*6.......(64 terms)) > 1 so 3 ^ (5^3) > 6 ^ ( 2^6)
3^125 = 3^(5x25) = (3^5)^25 = 243^25.
6^64 = 6^(3x21.3) = (6^3)^21.3 = 216^21.3.
243^25 > 216^21.3
Therefore, 3^(5^3) > 6^(2^6).
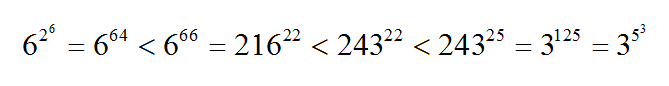
Remembering that order of operations requires us to work from the top down with exponents, we need to compare 3 1 2 5 and 6 6 4 = 2 6 4 ⋅ 3 6 4 .
Note that 3 1 2 5 > 2 6 4 ⋅ 3 6 4 if 3 6 1 > 2 6 4 . This is true (and can be shown via @Aareyan Manzoor 's method below), so 3 5 3 is larger!