Which has a larger area?
Geometry
Level
2
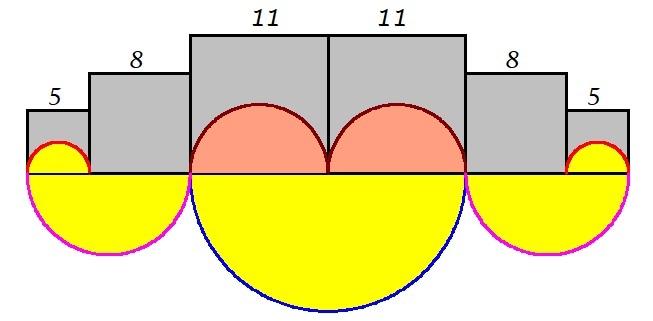 In the above figure, the side lengths of each square are given and all arcs are semicircles. Which has a larger area, the yellow region or the gray region?
In the above figure, the side lengths of each square are given and all arcs are semicircles. Which has a larger area, the yellow region or the gray region?
They are equal.
Gray region
Yellow region
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The yellow region is composed of semi circles. The diameter of each semicircle are the side lengths of the squares. We can used the formula A = 2 1 4 π d 2 where d is the diameter. Note that we multiplied by 2 1 because it is a semicircle. So the area of the yellow region is
A y e l l o w = 2 1 4 π ( 5 2 ) ( 2 ) + 2 1 4 π ( 1 3 2 ) ( 2 ) + 2 1 4 π ( 2 2 2 ) = 4 2 5 π + 4 1 6 9 π + 4 2 4 2 π = 1 0 9 π ≈ 3 4 2 . 4 3
It follows that the area of the gray region is
A g r a y = [ 5 2 − 2 1 4 π ( 5 2 ) ] ( 2 ) + ( 8 2 ) ( 2 ) + [ 1 1 2 − 2 1 4 π ( 1 1 2 ) ] ( 2 ) = 5 0 − 6 . 2 5 π + 1 2 8 + 2 4 2 − 3 0 . 2 5 π = 4 2 0 − 3 6 . 5 π ≈ 3 0 5 . 3 3