Which inequality should I apply?
2 x + y + z x + x + 2 y + z y + x + y + 2 z z
Let x , y and z be positive numbers. Find the maximum value of the expression above.
The answer is 0.75.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Moderator note:
There's a much simpler approach by applying AM-HM.
Hint : Normalize it. WLOG x + y + z = 1 .
B y a p p l y i n g R a v i S u b s t i t u t i o n , w e g e t x + y = a , y + z = b , z + x = c , S o i n e q u a t i o n w e g e t ∑ 2 ( a + c ) a + c − b o r ∑ ( 2 1 − 2 ( a + c ) b ) T h e s e c o n d p a r t i s N e s b i t t ′ s i n e q u a l i t y S o w e g e t m a x a s 2 3 − 4 3 = 4 3 ( a n s . )
Please excuse my inexperience, but why do you 'assume' that x+y+z= 1? Please explain, thankyou!
Log in to reply
Dear Rico Thank you for your query. As you can see, when we take x+y+z=s in the solution,the 's' cancels out in the solution which confirms that we can take x+y+z to be any number as it does not affect our evaluation. Now you may ask how would you know it without solving this inequality that we could take any value of (x+y+z) and solve this. Suppose that x,y,z are such that x+y+z=1.Now if you take x'+y'+z'=2, then then your x', y',z' would be 2x, 2y and 2z. If you take x'+y'+z'=s, then x'= sx, y'=sy, z'=sz. Put these values in original expression and verify. So we can assume WLOG that x+y+z=1. Hope it helps! If you have any queries, feel free to write to me at rdravi110@gmail.com
Best Wishes, Ravi Dwivedi
@Rico Lee Suppose that x + y + z = a , then $\frac{x}{a}+\frac{y}{a}+\frac{z}{a}=1$, now replace $x,y,z$ in the original expression by $\frac{x}{a},\frac{y}{a},\frac{z}{a}$, observe that the expression remains unchanged. In other words, let $E(x,y,z)$ be the given expression, then $E(\frac{x}{a},\frac{y}{a},\frac{z}{a})=E(x,y,z)$.
Here's my solution:
Let x + y + z = 1 . Then, the expression reduces to c y c ∑ 1 + x x let f ( x ) = 1 + x x . Since f ( x ) is a concave function, by Jensen's Inequality, we have f ( 3 x + y + z ) ≥ 3 f ( x ) + f ( y ) + f ( z ) thus, the minimum value of the expression is 3 × 4 1 = 0 . 7 5
Why is f(x) concave?
What do you mean?
Just apply the convex and concave verification rules
Which rules?
Just take f " ( x )
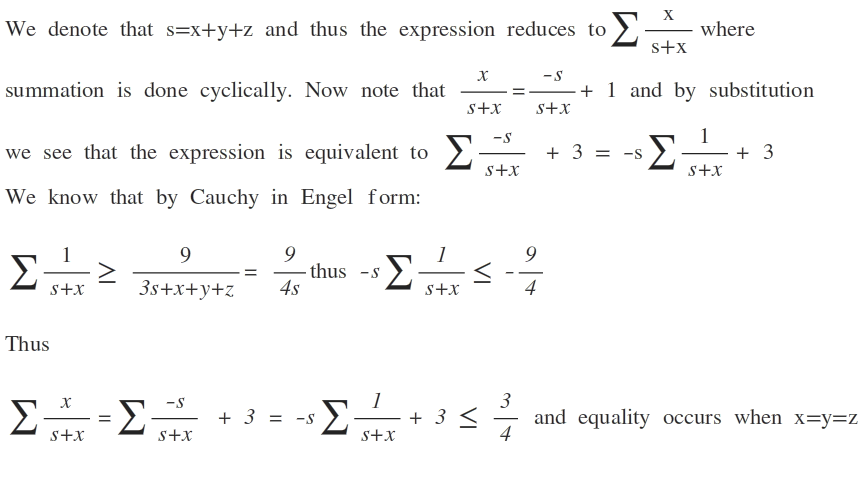Cauchy :) Note that the summation is cyclic
I will use Jensen's inequality
.