Which log is "heavier"?

Algebra Level 1

log ⁡ 3 4 , log ⁡ 4 5 \large\log_3 4 \qquad , \qquad \log_4 5

Which of these numbers is larger in value?

Image Credit: Wikimedia IllestFlip .
log ⁡ 3 4 \log_{3} 4 log ⁡ 4 5 \log_{4} 5

View wiki
Hobart Pao by Hobart Pao , 23, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

10 solutions

Raj Rajput
Jul 14, 2015

10 Helpful 0 Interesting 0 Brilliant 0 Confused

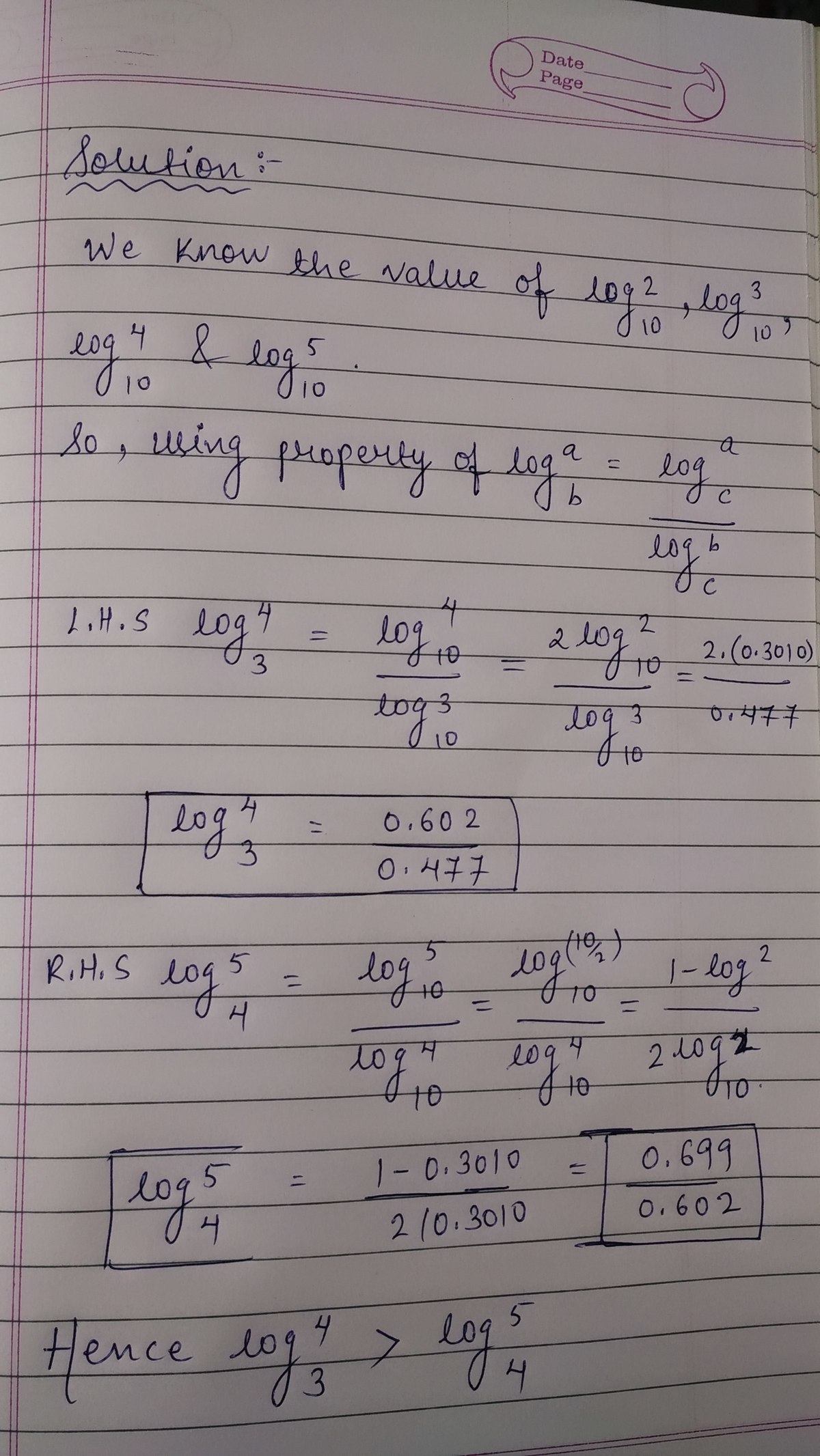
Moderator note:

Is there a way to solve this without logarithmic tables?

Nice handwriting!

Mike Roscope - 5 years, 11 months ago
Blackpen Redpen
Jul 14, 2015

6 Helpful 0 Interesting 0 Brilliant 0 Confused

Moderator note:

Yes. This is the generalization via calculus.

For simplicity sake, can you solve this simply based on the fact that both functions f ( x ) = 3 x f(x) = 3^x and g ( x ) = 4 x g(x) = 4^x are concave upwards?

J Dotson
Sep 30, 2015

Awesome solutions.

0 Helpful 0 Interesting 0 Brilliant 0 Confused
Rohan Naidu
Aug 5, 2015

Observe that the derivative of the function log x is proportional to 1/x, a monotonically decreasing function on positive reals. This means the rate at which log x is increasing is decreasing, that is, log x grows more between 3 and 4, than between 4 and 5. Therefore, log 4 is greater than log 3 by more than log 5 is greater than log 4...which leads to the desired result.

0 Helpful 0 Interesting 0 Brilliant 0 Confused
汶良 林
Jul 29, 2015

0 Helpful 0 Interesting 0 Brilliant 0 Confused
Chenjia Lin
Jul 25, 2015

My idea was to convert l o g 3 4 log_3 4 into 3 n = 4 3^{n} = 4 , and l o g 4 5 log_4 5 into 4 n = 5 4^{n} = 5 . Instead of finding n n in both equations, I plugged in 2 2 for the value of n. ignoring the right side of the equations. The result from plugging in 2 2 gave me a larger value for 4 n = 5 4^{n} = 5 .

0 Helpful 0 Interesting 0 Brilliant 0 Confused
Lew Sterling Jr
Jul 16, 2015

0 Helpful 0 Interesting 0 Brilliant 0 Confused
Tanishq Bhatia
Jul 16, 2015

Well, the way I saw this was that it is easier to increase a number by 1/4th than by 1/3rd.This means that the power to 4 to get 5 would be less than the power required for 3 to make it 4.

0 Helpful 0 Interesting 0 Brilliant 0 Confused

Moderator note:

You can't do that with logarithms.

That was my reasoning also. Isn't it valid ?

Louis LeLouis - 5 years, 7 months ago
Ayan Bhuyan
Jul 15, 2015

Let 3^x=4 and 4^y = 5. So, x/y=log5/log3 => x>y.

0 Helpful 0 Interesting 0 Brilliant 0 Confused

Moderator note:

Wrong. Check your working again.

Thiago Alves
Jul 15, 2015

0 Helpful 0 Interesting 0 Brilliant 0 Confused

Moderator note:

Check your working again. It's wrong.

Your approach is no different from interpreting the values from a logarithmic table.

Note: It is not "determinator", but "denominator" and it is positive.

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...