Which Platonic solid is in the middle?

Geometry Level 3

If each of the Platonic solid is circumscribed exactly within a given sphere then sorted into volume order, then which Platonic solid is in the middle of the list?

Dodecahedron Impossible to determine Icosahedron Cube Tetrahedron Octahedron

A Former Brilliant Member by A Former Brilliant Member

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

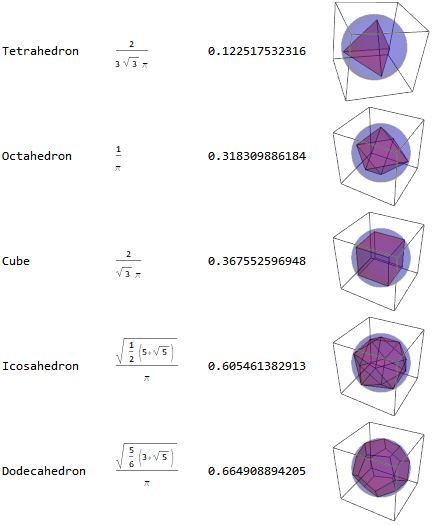
In a sphere of volume 1, here are the respective volumes: Tetrahedron 0.122518 Octahedron 0.31831 Cube 0.367553 Icosahedron 0.605461 Dodecahedron 0.664909 \begin{array}{ll} \text{Tetrahedron} & 0.122518 \\ \text{Octahedron} & 0.31831 \\ \text{Cube} & 0.367553 \\ \text{Icosahedron} & 0.605461 \\ \text{Dodecahedron} & 0.664909 \\ \end{array}

The same data redone to be more helpful:

1 Helpful 1 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...