Which Pocket Will It End Up In?

Geometry Level 3

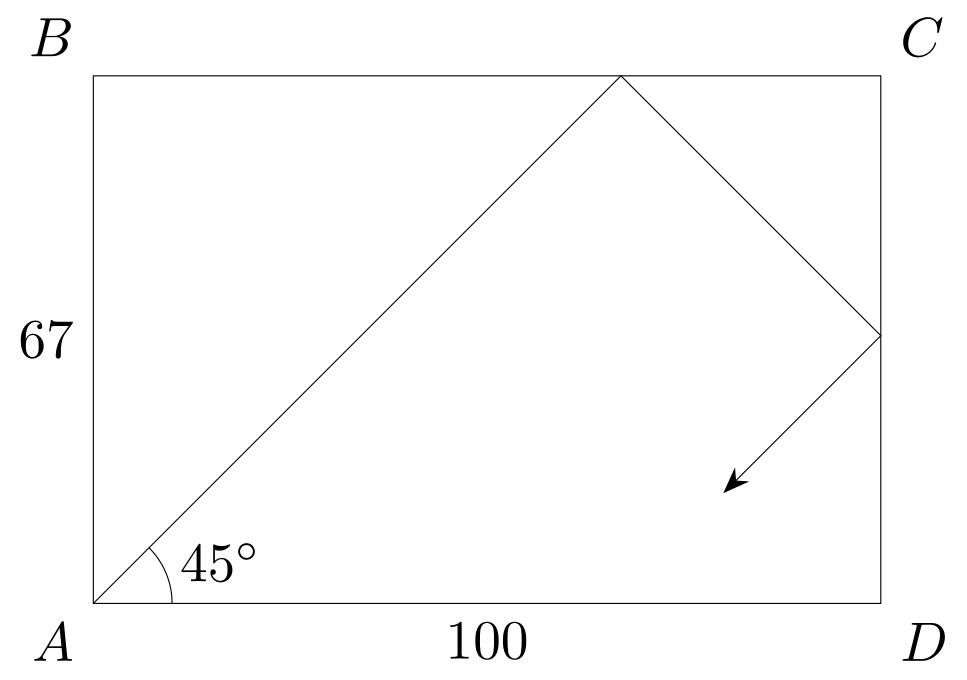
If you shoot a billiard ball as shown in the diagram, which pocket will the ball end up in?

Assume the ball only lands in a pocket if the center of the ball meets the corner of the pocket exactly.

Model the ball as a point mass.

A B C D The ball will never land in a pocket

2 solutions

Chitrank Gupta
Mar 7, 2016

We very well know of reflection property. Now what you have thought is that whenever ball strikes any mirror than it (apparently) enters into a rectangle which is just mirror image of it.

Now just keep on constructing rectangles with taking common sides $CD$ and $BC$ (initially) then their reflections too. now remember one thing that the ball will keep on moving in its direction until it reaches one of the vertices of our apparent rectangles. and hence it is obvious that the no. of such apparent rectangles that you will need in the horizontal direction will be 67 and in the vertical direction is 100 (smallest possible). being 67 odd hence, it is obvious that it will fall either in $C$ or $D$ and 100 being even it will eventually fall into $D$ .

Do you feel that this problem corresponds to level 4 Geometry category ? I think it should be a logic problem

Aakash Khandelwal - 5 years, 3 months ago

I would agree with the solution if it would be a rectangle, with corners and not a billiard table with pockets. We all know that a little error of the shot is not important at billiard and the ball will hit the pocket.

Andi Popescu - 5 years, 3 months ago

Do you have any other solution ?

Rohan Jasani - 5 years, 3 months ago

Very good way of solving. I never thought in this way! Up voted. Is it C, D as you have put or B, D ?

Niranjan Khanderia - 5 years, 3 months ago

I don't see how this can be correct. The number of times it will bounce in the vertical direction is 67/gcd(67,100)-1=66, which means it should be travelling upwards after the final bounce and the amount of times it bounces horizontally is 100/gcd(67,100)-1=99, which means it should be moving leftwards after the final bounce. But that would indicate that it lands in pocket B. What am I missing here?

Tristan Goodman - 5 months, 1 week ago

Omar Monteagudo
Mar 14, 2016

This problem remind me something I read once called " Máquina de Zavrotsky ". There is an amazing connection between this problem and gcf(67, 100).

Which Pocket Will It End Up In?

2 solutions

0 pending reports