Which point is which?
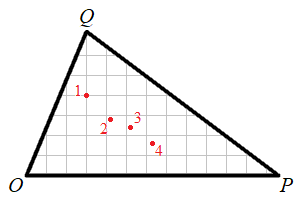ΔOPQ has vertices O(0, 0), P(12.6, 0), and Q(3, 7.2).
Lying in the interior of ΔOPQ are the following points:
Point 1: (3, 4),
Point 2: (4.2, 2.8),
Point 3: (5.2, 2.4), and
Point 4: (6.3, 1.6).
Write the four-digit number in which the first digit corresponds to the centroid,
the second digit corresponds to the circumcenter,
the third digit corresponds to the incenter,
and the fourth digit corresponds to the orthocenter of ΔOPQ.
The answer is 3421.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
The centroid is the ordered pair (average(x), average(y)), or (5.2, 2.4)... point 3. The circumcenter is the point of concurrency of the perpendicular bisectors of each side. The perpendicular bisector of O P is the line x = 6.3, on which point 4 lies. The incenter of a triangle that's not isosceles will not fall on the Euler line of the triangle, the the only one of the four points not colinear with the others is point 2. The orthocenter is the point of concurrency of the altitudes. The altitude on O P through Q is the line x = 3, on which point 1 lies. The number is 3421.