Which Route Should I Take?

Geometry Level 2

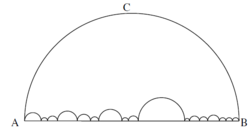When you travel from A to B, you can either travel along the big semi-circle (i.e. via C) or you can travel along all the smaller semi-circles. Which is the shorter route and why?

Problem 5 on South African Mathematics Olympiad Junior Round 3 Paper 2012

The big semi-circle (via C) Both routes have the same distance The smaller semi-circle

Mark Mottian by Mark Mottian , 22, South Africa

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Caleb Townsend
Apr 10, 2015

The length of the path through C C is half the circumference of the corresponding circle, i.e. π 2 × d . \frac{\pi}{2}\times d.

The length of the path through the small semicircles is the sum of the individual lengths of each semicircle, i.e. π 2 × d 1 + π 2 × d 2 + π 2 × d 3 + . . . = π 2 × ( d 1 + d 2 + d 3 + . . . ) \frac{\pi}{2}\times d_1 + \frac{\pi}{2}\times d_2 + \frac{\pi}{2}\times d_3 + ... \\ = \frac{\pi}{2}\times(d_1 + d_2 + d_3 + ...) Also the diameter of the big semicircle is quite obviously equal to the sum of diameters of the smaller semicircles. So this length is also π 2 × d . \frac{\pi}{2}\times d. The paths have equal length.

1 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...