Which Statements Are True?

For I, $f(0) > 0, f(1) < 0, f(2) > 0$ implies there are at least two solutions by IVT .

For II, $x=0$ is clearly a solution, and the function $f(x) = x-\sin(x)$ has derivative $1-\cos(x),$ which is nonnegative everywhere, so $f$ is increasing everywhere, so there is only one solution.

For III, an odd-degree polynomial always has at least one real root (if the leading coefficient of $f$ is positive, then $f(x)$ is negative for negative enough $x$ and positive for positive enough $x$ ), and this one has exactly one because its derivative is $15x^4-60x^2+60 = 15(x^2-2)^2,$ which is always nonnegative.

For IV, $x=0$ is a solution, and there is also a solution between $x=\pi$ and $x=3\pi/2,$ because $\tan(x)-x = -\pi$ for $x=\pi$ but $\tan(x)-x$ gets arbitrarily large as $x$ approaches $3\pi/2.$ Since $\tan(x)-x$ is continuous on $[\pi,3\pi/2),$ there will be a root on that interval as well. (Note that the derivative is nonnegative everywhere, but the function $\tan(x)-x$ is discontinuous at lots of different places.)

So the answer is II and III only.

This is a partial solution. But one way to solve this is to graph the functions. 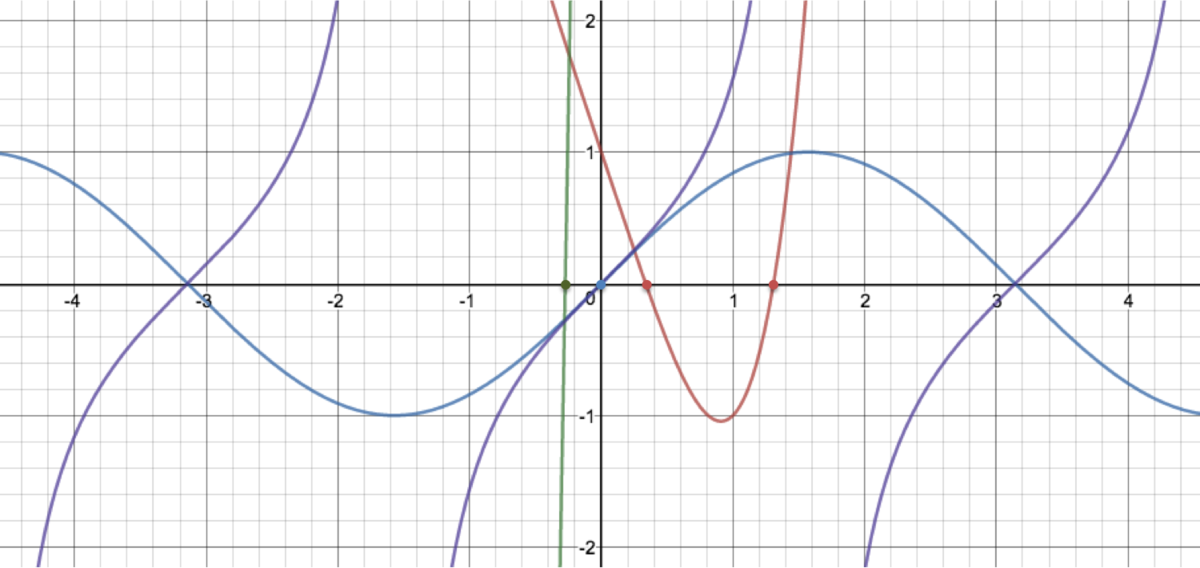The first function is represented by the red line, and is disqualified because there is no unique solution, the function crosses the x-axis, i.e. $y=0$ at two points.
The second function clearly has a real solution, $(0,0)$ , as $sin(0) = 0$ . And scanning the graph makes it look as if this is the only, unique, solution.
The third function is the green one, which clearly does cross the x-axis at one real point. And expands infinitely from there, so is unique.
The fourth function clearly has at least one real solution, $(0,0)$ , however it's also apparent that each instance of $tan(x)$ , for instance $tan(x)$ bounded by $y=0$ and $y=5$ there is some point where $tan(x)=x$ , so it's not unique.

let's focus one-by-one on each option:

I. for the equation $let g(x) = x^4-3x+1$ . By some observation, we get that: $g(0) > 0, g(1) < 0, g(2)> 0$ which by the *Intermediate value theorem * tells us that $x^4-3x+1 = 0$ have minimum 2 solution. So we won't choose any option that have (I)

II. for $sin x = x$ , notice that the gradient of tangent line on $x = 0$ is 1, which tells us that $sin x = x$ will have only 1 solution, that is $x=0$

IV. $tan(x) = x$ clearly have many solutions (you can interpret it graphically.

III. left for reader as a practice