Which Step Does It Land On?
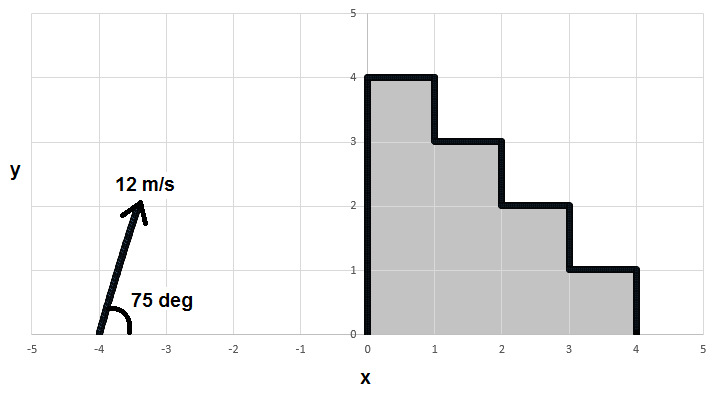
A projectile is launched from an initial position ( x , y ) = ( − 4 m , 0 m ) . The projectile's initial speed is 1 2 m/s and it is launched at a 7 5 ° angle with respect to the x -axis. There is a staircase with 4 steps, as pictured above. The top step begins at ( x , y ) = ( 0 m , 4 m ) meters and the bottom step ends at ( x , y ) = ( 4 m , 0 m ) . Each step is 1 m wide and 1 m deep. The projectile flies over part of the staircase and lands on one of the steps. What is the x coordinate of the landing point in meters?
Details and Assumptions
- The gravitational acceleration is in the − y direction, with a magnitude of 9 . 8 m s − 2 .
The answer is 2.7649.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
why do we added x+4 in the first eq ;how is y=12sin...........
Relevant wiki: 1D Kinematics Problem Solving
I assume that everyone knows how to solve 2D kinematic equations, so here's a rough outline of the solution.
1) Based on the x velocity, determine the two times (tx) at which the projectile passes over the x boundaries of each step.
2) Based on the initial y velocity and the influence of gravity, determine the second instance in time (ty) at which the projectile y position matches the altitude of each step. The first instance in time corresponds to a negative x value, and is thus useless.
3) If the solution to (2) is between the two numbers from (1), we have a candidate intersection.
4) Find the highest (in terms of y position) step with a candidate intersection.
5) Find the projectile x coordinate corresponding to the time of intersection with the staircase step from (4)
The solution spreadsheet and projectile plot are given below:
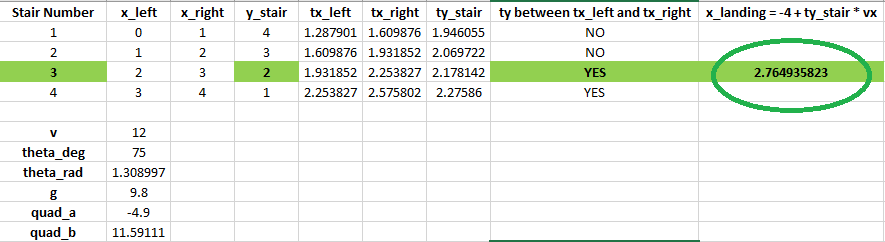
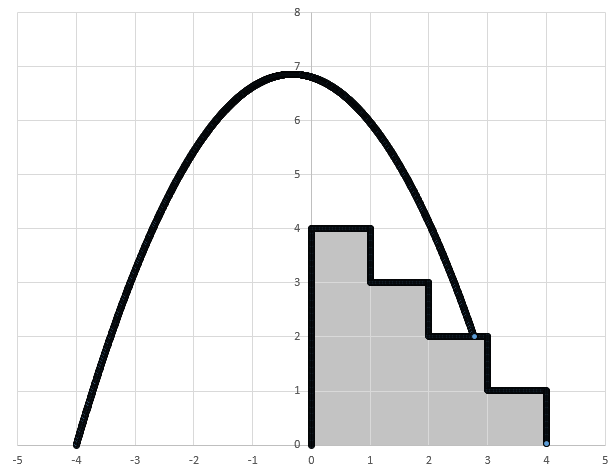
what is this ? i entered 2.68 as the answer and it gave wrong and wrong again, i took some approximations to some points and got 2.68 it should consider my answer also
Log in to reply
I suppose that depends on the error margin that is built into Brilliant's code for decimal answers. I actually don't know what that is.
I used desmos. We know that the equation of a projectile is given by
:
y
=
x
tan
θ
(
1
−
R
x
)
. You can find a proof
here
.
Also, the range (
R
) of this projectile is
g
v
0
2
sin
(
2
θ
)
=
g
7
2
. Graphing this at the given values gives us a path that looks like -
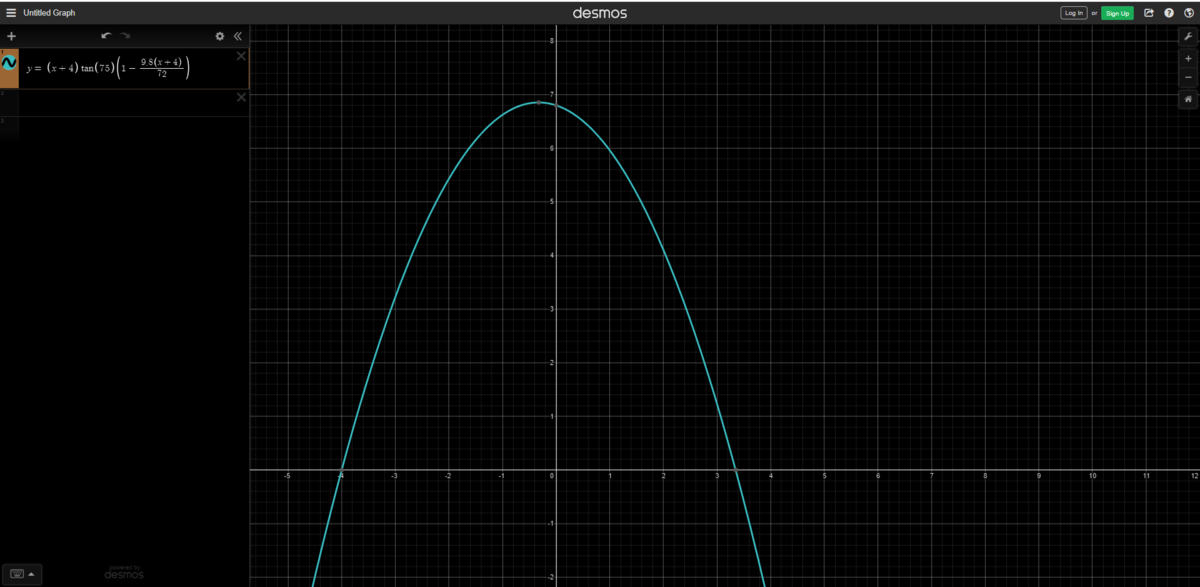
Just by eyeballing it, we can see that x ≈ 2 . 7 .(you can draw the steps if you like).
We observe that the x coordinate of the projectile can be expressed as such: x = 1 2 cos 7 5 ∘ t t = 1 2 cos 7 5 ∘ x + 4
Then, we observe that the y coordinate of the projectile can be expressed as such: y = 1 2 sin 7 5 ∘ t − 2 g t 2
Substituting the first equation into the second, we find that y = 2 8 8 cos 2 7 5 ∘ − g x 2 + ( tan 7 5 ∘ − 2 8 8 cos 2 7 5 ∘ 8 g ) x − 1 8 cos 2 7 5 ∘ g
Then, by observing the graph, we can deduce that the answer is 2.765. One may use desmos for this.