Which Triangle is Larger?
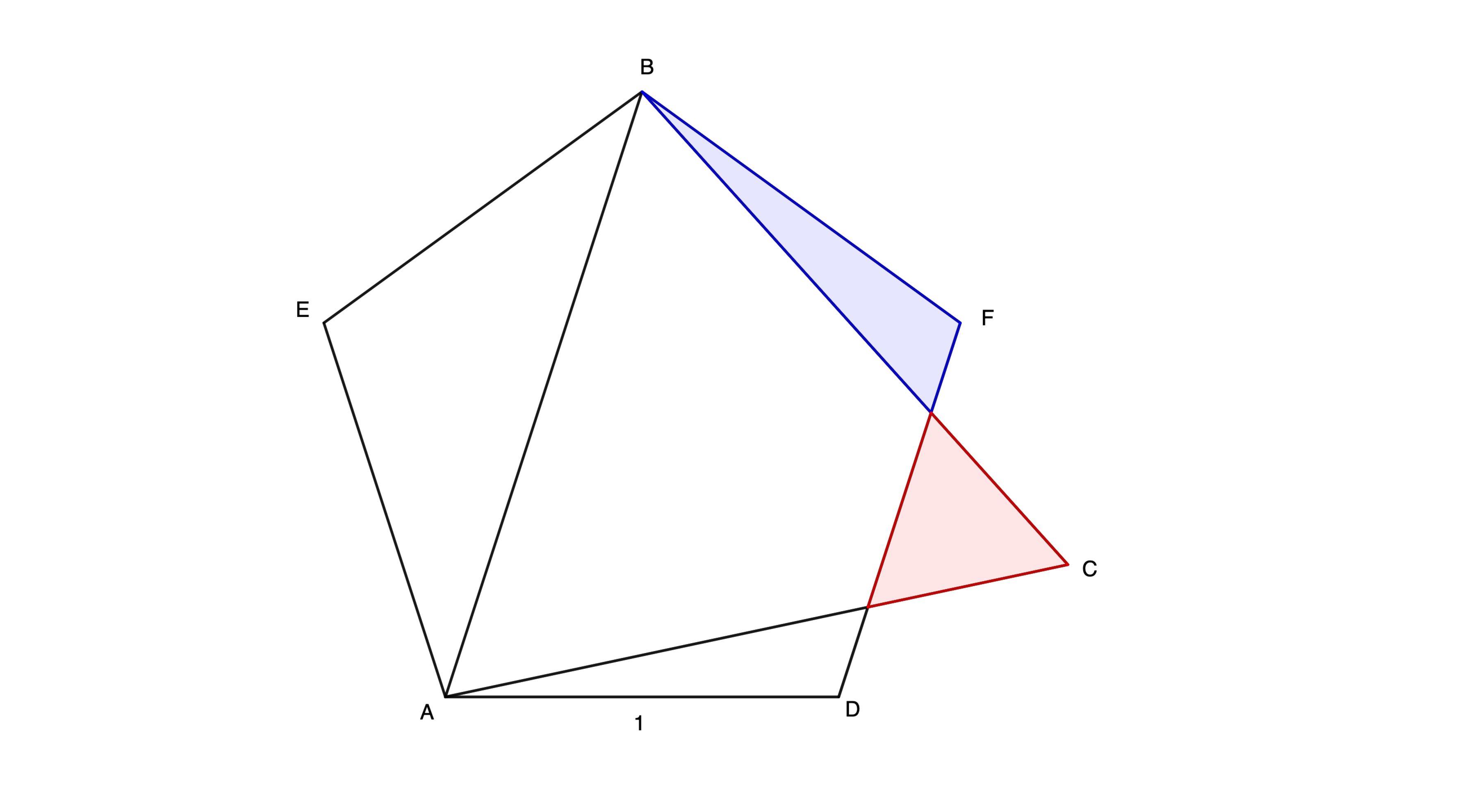
is a regular pentagon of side length 1. is an equilateral triangle with a side congruent to the pentagon's diagonal. Which triangle, red or blue, has the larger area? For extra credit, provide closed-form representations of the areas of the red and blue triangles.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
All angles are in degrees.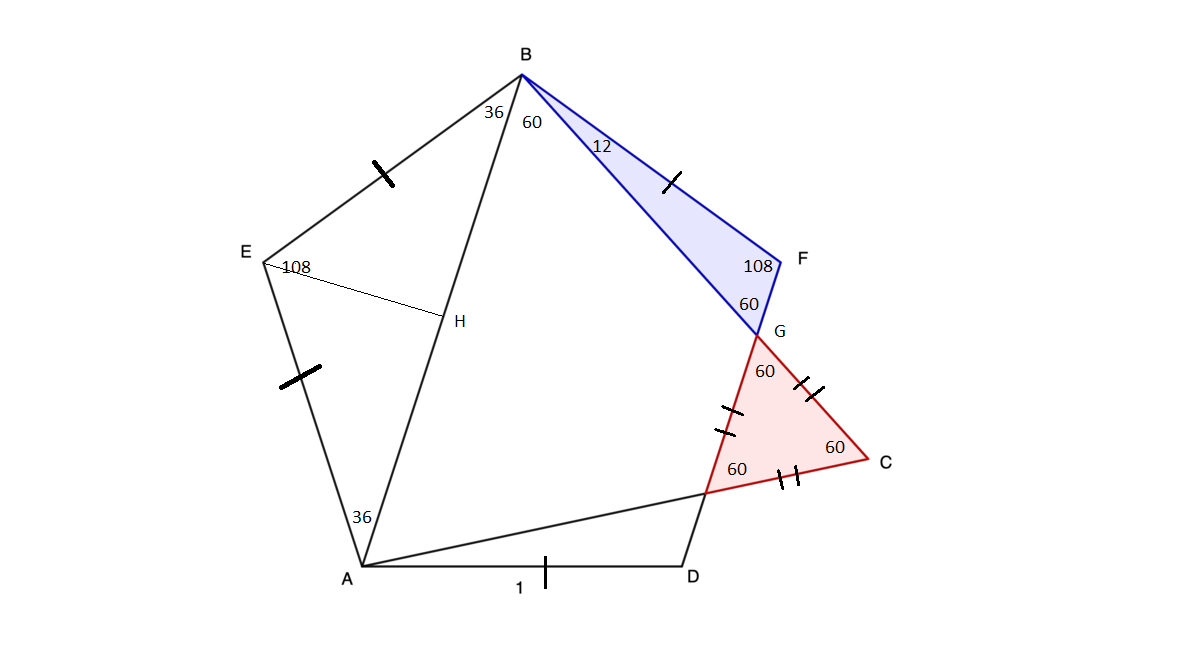
Line segment
E
H
divides
△
A
B
E
into two congruent right triangles. This gives the length of
A
B
as
A
B
=
2
⋅
1
⋅
cos
(
3
6
)
=
2
cos
(
3
6
)
Using the sine rule on
△
B
F
G
, we can calculate the sides
F
G
and
B
G
.
sin
(
6
0
)
1
=
sin
(
1
2
)
F
G
=
sin
(
1
0
8
)
B
G
F
G
=
sin
(
6
0
)
sin
(
1
2
)
B
G
=
sin
(
6
0
)
sin
(
1
0
8
)
Since
△
A
B
C
is equilateral,
B
G
+
G
C
=
A
B
. Consequently,
G
C
=
A
B
−
B
G
=
2
cos
(
3
6
)
−
sin
(
6
0
)
sin
(
1
0
8
)
Use the area formula
A
=
2
1
a
b
sin
(
C
)
on both the blue and red triangles.
A
(
blue
)
=
2
1
⋅
1
⋅
sin
(
6
0
)
sin
(
1
2
)
⋅
sin
(
1
0
8
)
≈
0
.
1
1
4
A
(
red
)
=
2
1
⋅
(
2
cos
(
3
6
)
−
sin
(
6
0
)
sin
(
1
0
8
)
)
2
⋅
sin
(
6
0
)
≈
0
.
1
1
7
Therefore, the red triangle has a larger area than the blue triangle.