White Dot, Black Dot
The diagram below shows a 2 × 1 0 grid of dots (of negligible size) that alternate between black and white. How many ways are there to draw ten line segments between the dots such that
- each white dot is connected to exactly one black dot (and vice versa),
- no segment passes through more than two dots, and
- none of the segments intersect each other?
Bonus: Generalize for drawing n segments on a 2 × n grid, where n is a positive integer.
The answer is 2317.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
In your solution, let us label the columns (x) from left to right, 1 to 10 and the rows (y) from bottom upwards 1 and 2. In the second drawing, what is keeping the white dot (1,1) to connect with black (7,2), thus connecting (3,2) with (4,2) and (6,1) with (10,2) leaving (9,1) and (10,1) together ?
Log in to reply
We are assuming a fixed number of horizontal segments in each row - in this case, 3. Connecting (1, 1) to (7, 2) will force us to draw additional horizontal segments in both rows, which would not be allowed.
Top keep the solution general, let N = 1 0 .
I started my solution similar to that of Steven: In each row, we can freely choose connected pairs of neighboring dots, provided that we choose the same number of pairs in the top row and the bottom row. The remaining dots may now be connected across the rows by a vertical or diagonal segment.
To count the number of ways to choose the neighboring dots, think of the individual dots as "stars" and the chosen pairs as "bars". It is generally known that s stars and b bars may be placed in ( b s + b ) ways. Applying this here, if b = n is the number of horizontal pairs in each row, then there are s = N − 2 n individual dots left, so that there are ( n N − n ) ways to select n horizontal pairs in each row . Since we must choose this configuration independently in each of the rows, we take the square; then sum over the possible number of horizontal pairs: A ( N ) = n = 0 ∑ ⌊ N / 2 ⌋ ( n N − n ) 2 .
Substituting A ( 1 0 ) we obtain A ( 1 0 ) = ( 0 1 0 ) 2 + ( 1 9 ) 2 + ( 2 8 ) 2 + ( 3 7 ) 2 + ( 4 6 ) 2 + ( 5 5 ) 2 = 1 2 + 9 2 + 2 8 2 + 3 5 2 + 1 5 2 + 1 2 = 2 3 1 7 .
Note that the sequence A ( N ) is known as the Whitney numbers of the second kind .
Note also that the calculation can be illustrated in Pascal's Triangle. Square the circled numbers and add:
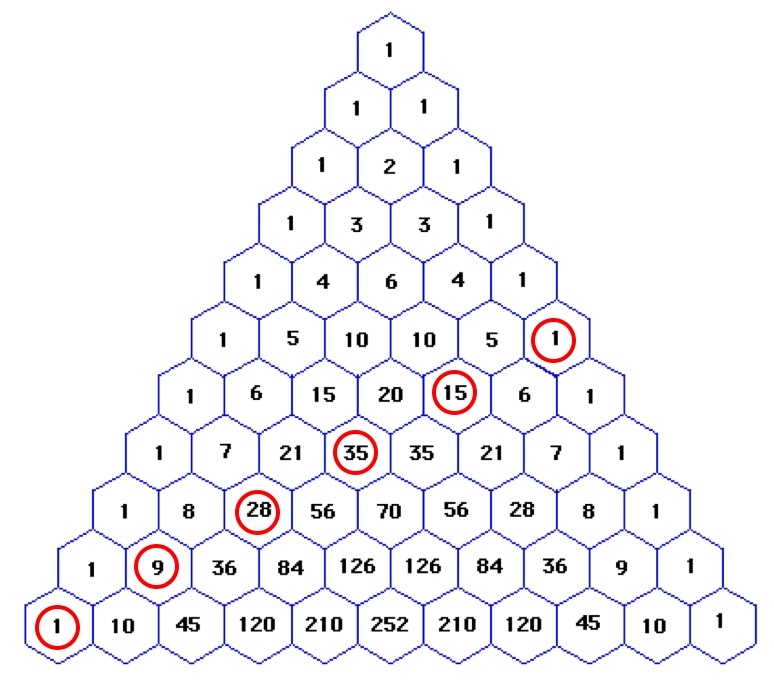
And if you wouldn't square, the circled numbers would add up to the Fibonacci numbers.
The following recursive algorithm could be used if it was difficult to come up with the right solution analytically
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
|
The first key realization is that there must be the same number of horizontal segments in the top row as in the bottom row . Otherwise, after the dots are paired off vertically and diagonally, there will be some number of dots left in one row, which either can be connected to form the missing horizontal segments or are un-connectable.
The second key realization is that given a fixed number of horizontal segments in each row, for each possible arrangement of horizontal segments, there is exactly one way to draw the remaining segments . To see why this is, let's take this combination of horizontal segments with a fixed 3 horizontal segments in both the top and bottom rows:
Consider the leftmost unconnected dot in the arrangement, which is the white dot in the bottom row. The only dot that this white dot can connect to is the leftmost black dot on the top row, because any other connection will block the other dots from forming horizontal or diagonal segments. Thus, we must do this:
Then, we take the next leftmost dot of the arrangement and repeat the same process over and over. We end up with this arrangement:
Note that the segments we drew were forced; we could not pair up the dots in any other way without introducing more horizontal segments or leaving some dots unconnected. Thus, for each combination of a fixed number of horizontal line segments in each row, there is only one way to connect the other dots.
Combining our observations, to count the total number of ways to connect the dots, we count the number of ways to draw a fixed number h of horizontal segments in one row, square that number, and finally sum those squared terms over all possible values of h .
Since we have 10 dots in a row, 0 ≤ h ≤ 5 . The cases of h = 0 and h = 5 are easy; there's only one way to connect the remaining dots for both cases, so the number of ways to draw the segments for each case is 1 2 . The case of h = 1 is also straightforward: there are 9 ways to draw exactly one horizontal segment in one row, so there's 9 2 ways to draw the rest of the segments.
Suppose 2 ≤ h ≤ 4 . If we draw the horizontal segments from left to right, we see that drawing h horizontal segments is the same as choosing h starting points for the segments. There are only 9 possible starting points to draw each segment, which are the first 9 dots in the row.
Now, we will make a bijection between choosing the starting points and a stars and bars argument. Because each dot can only be connected to one other dot, the starting points must be spaced at least one apart from each other. Let a 1 , a 2 , … , a h + 1 be nonnegative integers such that a i represents the number of dots between the ( i − 1 ) th starting point and the i th starting point. (Points 0 and h + 1 are the beginning and end of the row, respectively.) Since starting points must be spaced at least one apart, we have a 2 , a 3 , … , a h ≥ 1 . Because h of the dots must be starting points, the sum of all the gaps must be equal to 9 − h :
a 1 + a 2 + a 3 + ⋯ + a h + 1 = 9 − h .
Let a i ′ = a i − 1 for 2 ≤ i ≤ h . We can rewrite the equation above as
a 1 + ( a 2 ′ + 1 ) + ( a 3 ′ + 1 ) + ⋯ + a h + 1 a 1 + a 2 ′ + a 3 ′ + ⋯ + a h + 1 + ( h − 1 ) a 1 + a 2 ′ + a 3 ′ + ⋯ + a h + 1 = 9 − h = 9 − h = 1 0 − 2 h .
Each of the terms is nonnegative, so by stars and bars, the number of ways to assign values to each is ( h ( 1 0 − 2 h ) + h ) = ( h 1 0 − h ) . Because each variable represented a gap between starting points, ( h 1 0 − h ) is also the number of ways to choose starting points such that each starting point is at least one dot apart i.e. the number of ways to draw h horizontal segments in a row. Squaring this gives ( h 1 0 − h ) 2 ways to draw the remaining segments.
Finally, the total number of ways to draw the segments under the given rules is
1 2 + 1 2 + 9 2 + h = 2 ∑ 4 ( h 1 0 − h ) 2 = 1 + 1 + 8 1 + ( 2 8 ) 2 + ( 3 7 ) 2 + ( 4 6 ) 2 = 8 3 + 2 8 2 + 3 5 2 + 1 5 2 = 2 3 1 7 .
Note that the final sum is equivalent to h = 0 ∑ 5 ( h 1 0 − h ) 2 . In general, the number of ways to draw n segments between a grid of 2 × n dots is k = 0 ∑ ⌊ 2 n ⌋ ( k n − k ) 2 .