Who ate that apple? Dr. Worm ate it.
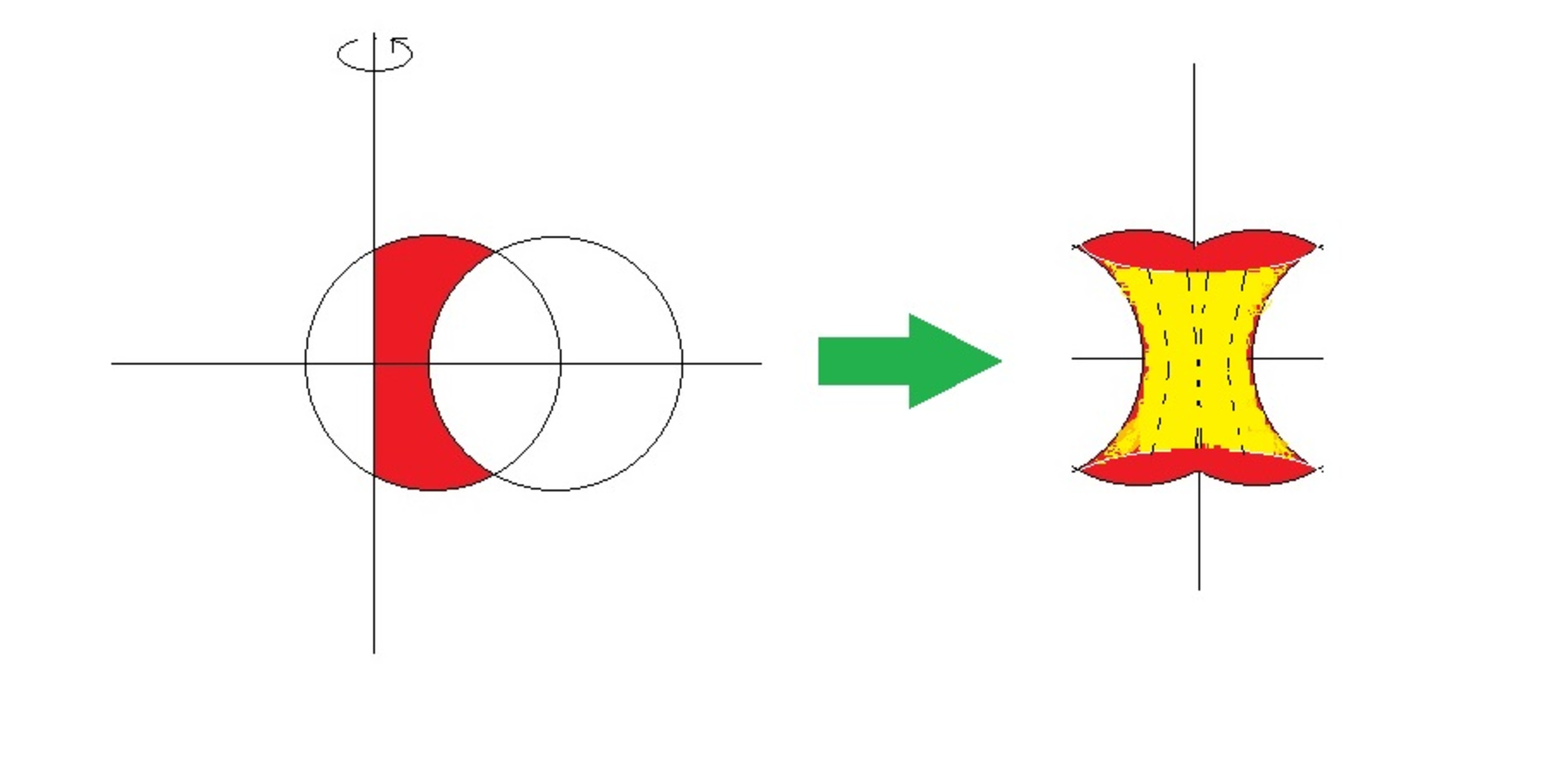
Two circle graphs of the same radius of 1 intersect each other's center, and the centers are points & respectively.
If the shaded area is rotated around the -axis to produce an "apple core" structure as shown above, what is the volume of this "apple core"?
Give your answer to the nearest 3 decimal places.
The answer is 2.943.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
In order to find the volume of revolution, let us divide the "apple core" into parts by the blue lines y = 2 3 and y = 2 − 3 .
The volume generated between the blue lines (called V 1 ) is bounded by the circle graph on the right: ( x − 1 . 5 ) 2 + y 2 = 1 .
Then x − 1 . 5 = − 1 − y 2 (Note that ( 0 . 5 , 0 ) is on the graph, so the sign must be minus.)
Hence, x 2 = 4 1 3 − 3 1 − y 2 − y 2 .
Then V 1 = ∫ 2 − 3 2 3 π ( x 2 ) d y
= 2 ∫ 0 2 3 π ( 4 1 3 − 3 1 − y 2 − y 2 ) d y
= 2 π [ 4 1 3 y − 2 3 ( a r c s i n ( y ) + y 1 − y 2 ) − 3 y 3 ∣ 0 2 3 ]
= 2 π ( 8 9 ( 3 ) − 2 π )
Now the volume above the blue line is created from the area bounded between the plus & minus signs of the graph: ( x − 0 . 5 ) 2 + y 2 = 1 .
Thus, the rest of the volume = 2 π ∫ 2 3 1 ( 4 5 + 1 − y 2 − y 2 ) − ( 4 5 − 3 1 − y 2 − y 2 ) d y
= 2 π ∫ 2 3 1 2 1 − y 2 d y
= 2 π [ a r c s i n ( y ) + y 1 − y 2 ∣ 2 3 1 ]
= 2 π [ 2 π − ( 3 π + 4 3 ) ]
Adding the parts together, the total volume = 2 π [ 8 7 3 − 3 π ] ≈ 2 . 9 4 3