Who developed the mod function?

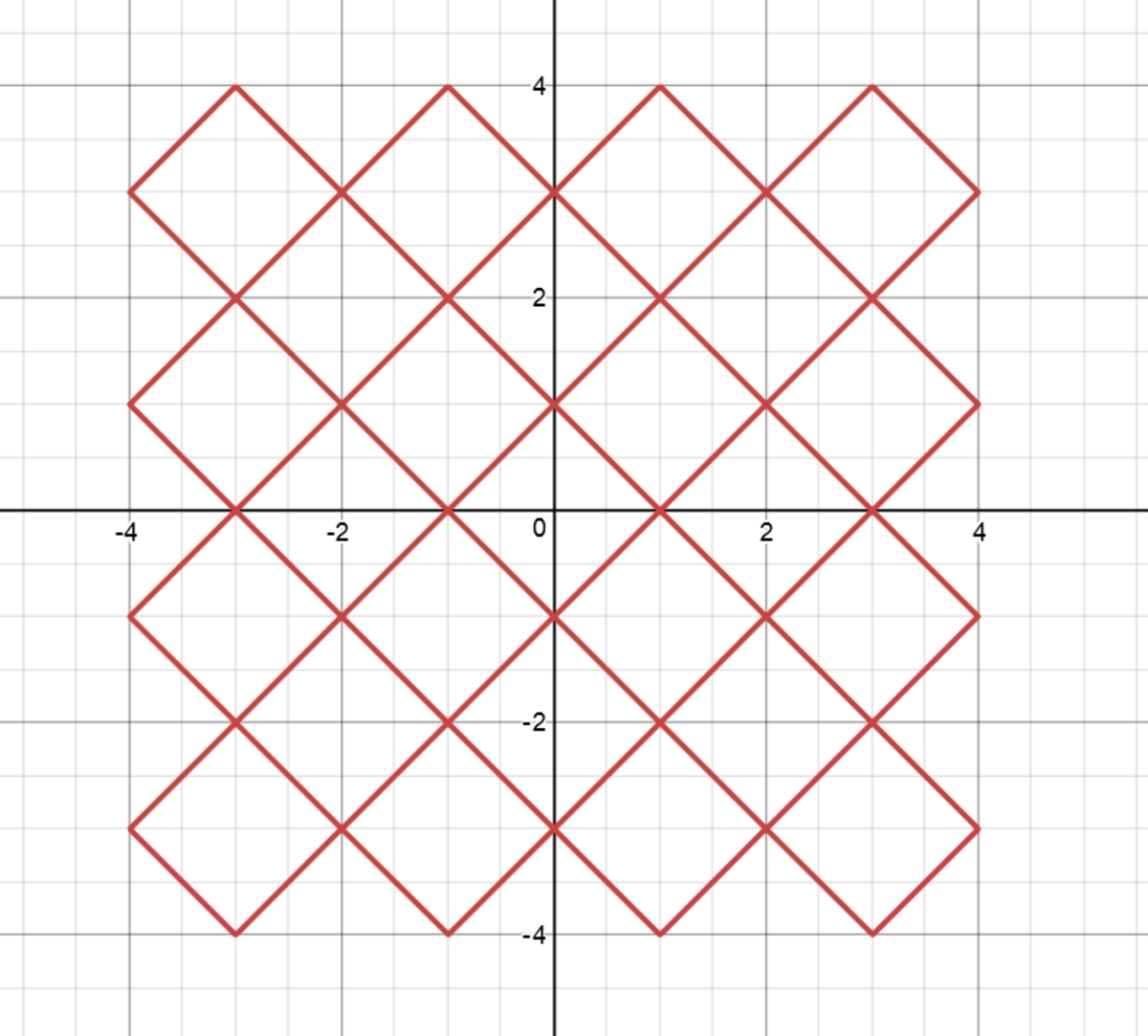
Substituting $x$ by $-x$ returns the same equation. Similarly substituting $y$ by $-y$ also returns the same equation. Therefore the graph represented by this equation is symmetrical about both the x and y axes and the length of the graph in all the quadrants is the same.

$\therefore$ The length of graph $=$ $4 \times$ the length of graph in the first quadrant.

In the first quadrant, $x>0$ and $y>0$ , $\therefore$ the equation reduces to $||x-2|-1|+||y-2|-1|=1$

Note that both $x$ and $y$ can only take values in the range $[0,4]$ , i.e. the graph lies in the square formed by the axes and the lines $x=4$ and $y=4$ .

Now, if we shift the origin to $(2,2)$ , the equation becomes $||x|-1|+||y|-1|=1$ , which is again symmetrical about both the axes. Therefore, the graph in the first quadrant can further be divided into 4 symmetric quadrants by the lines $x=2$ and $y=2$ :

• $2 \leqslant x \leqslant 4$ , $2 \leqslant y \leqslant 4$

• $0 \leqslant x \leqslant 2$ , $2 \leqslant y \leqslant 4$

• $0 \leqslant x \leqslant 2$ , $0 \leqslant y \leqslant 2$

• $2 \leqslant x \leqslant 4$ , $0 \leqslant y \leqslant 2$

$\therefore$ The length of graph $=$ $4 \times$ the length of graph in the first quadrant. $=$ $4^2 \times$ the length of graph in the region $2 \leqslant x \leqslant 4$ , $2 \leqslant y \leqslant 4$

In this region, the equation again reduces to $|x-3|+|y-3|=1$ whose graph is a square congruent to $|x|+|y|=1$ but centered at $(3,3)$ .

$\therefore$ The length of graph in the region $2 \leqslant x \leqslant 4$ , $2 \leqslant y \leqslant 4$
$=$ Perimeter of the square given by $|x|+|y|=1$

$=$ $4 \times \sqrt{2}$

$\therefore$ The length of graph $=$ $4^2 \times$ the length of graph in the region $2 \leqslant x \leqslant 4$ , $2 \leqslant y \leqslant 4$ $=$ $4^3\sqrt{2}$

The graph will be as follows :