Who is Correct ?
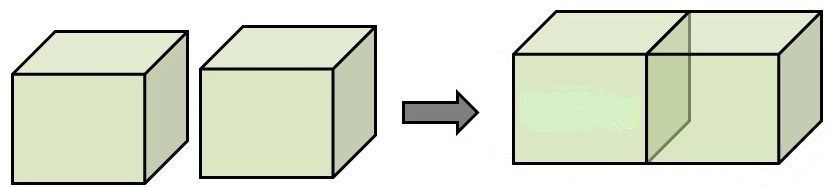
Three friends Alice, Bob, and Ram are in a room. Bob has made two identical cubes out of clay, and the surface area of each cube is 1 5 0 cm 2 . To test Bob, Ram joins the two cubes as shown in the diagram and asks him to calculate the new surface area. Just then Alice too joins the conversation. The three express different views on the new surface area:
- Bob: "It's simple! The new surface area is 3 0 0 cm 2 . "
- Ram: "You are wrong, Bob! The new surface area is 2 5 0 cm 2 . "
- Alice: "You are both wrong! The new surface area is 2 7 5 cm 2 . "
Who made the correct statement?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Surface area of a cube = 6 a 2 (as there are 6 surfaces each with area a 2 ).
Initially, there is only one cube, so 6 a 2 = 1 5 0 ⟹ a 2 = 2 5
But now two cubes are joined, that means we should neglect one surface from each cube (the surface of contact between the two) to get the new surface area.
⟹ 2 ( 6 a 2 ) − 2 ( a 2 ) = 1 0 a 2
∴ New Surface Area = 1 0 × 2 5 = 2 5 0
Hence, Ram made the correct statement
Of course Ram is right... (you wouldn't want Ram to be wrong, right?) :p
Log in to reply
Ha-ha. I have been seeing him do that before.
Log in to reply
Yes you both are correct. Not only me but everyone likes to do that.
I read the question after submitting Ram as the answer ;-)
Since Ram wants to test Bob if he can get the correct answer, Ram definitely should know what is the correct answer. So what Ram says is inevitably true. Hence, the answer will be 250.
The cube has 6 sides, surface area of 5 sides of the cube is (5/6)*150=125 square cm.
Therefore, new surface area of required cube is 2*125=250 square cm. Hence, Ram 's statement is true.
Two cubes have 12 faces, but when the 2 cubes are join as seen in the picture you see only 10 faces. To calculate how much is a faces divide 1 5 0 cm 2 (the surface area of a cube) on 6(the faces of a cube) and get 25 one face of a cube. 25 x 10 = 2 5 0 cm 2 (the new surface area). Ram's sentence is right.
Ram does not want to prove Ram wrong. Wait … is this confusing?